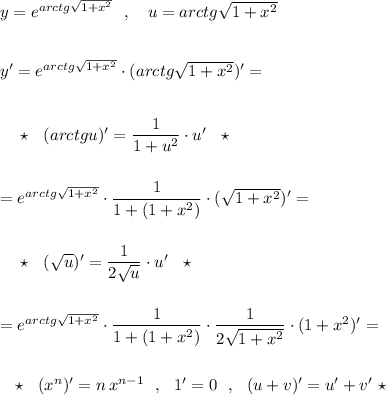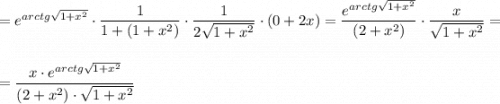Регистрация Спросить otvet5GPT
parus27
22.09.2020 18:50
Математика
Есть ответ 👍

Вычислить производную функции.

213
359
Посмотреть ответы 3

Ответы на вопрос:

Crazs
Crazs
4,8(39 оценок)

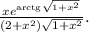
\frac{{x{e^{{\mathop{\rm arctg}\nolimits} \sqrt {1 + {x^2}} {{(2 + {x^2})\sqrt {1 + {x^2}} }}.

Пошаговое объяснение:

Это сложная функция. Берем производную сперва от e в степени, потом умножаем последовательно на производные вложенных функций: арктангенса, корня, квадрата:

{\left( {{e^{{\mathop{\rm arctg}\nolimits} \sqrt {1 + {x^2}} }}} \right)^\prime } = {e^{{\mathop{\rm arctg}\nolimits} \sqrt {1 + {x^2}} }} \cdot \frac{1}{{1 + 1 + {x^2}}} \cdot \frac{1}{{2\sqrt {1 + {x^2}} }} \cdot 2x = \frac{{x{e^{{\mathop{\rm arctg}\nolimits} \sqrt {1 + {x^2}} {{(2 + {x^2})\sqrt {1 + {x^2}} }}.

Наташа1111111124
Наташа1111111124
4,5(58 оценок)

Производная сложной функции   (e^{u})'=e^{u}\cdot u'  .

y=e^{arctg\sqrt{1+x^2}}\ \ ,\ \ \ u=arctg\sqrt{1+x^2}y'=e^{arctg\sqrt{1+x^2}}\cdot (arctg\sqrt{1+x^2})'={}\ \ \ \star \ \ (arctgu)'=\dfrac{1}{1+u^2}\cdot u'\ \ \star =e^{arctg\sqrt{1+x^2}}\cdot \dfrac{1}{1+(1+x^2)}\cdot (\sqrt{1+x^2})'={}\ \ \ \star \ \ (\sqrt{u})'=\dfrac{1}{2\sqrt{u}}\cdot u'\ \ \star =e^{arctg\sqrt{1+x^2}}\cdot \dfrac{1}{1+(1+x^2)}\cdot \dfrac{1}{2\sqrt{1+x^2}}\cdot (1+x^2)'={}\ \ \star \ \ (x^{n})'=n\, x^{n-1}\ \ ,\ \ 1'=0\ \ ,\ \ (u+v)'=u'+v'\ \star

=e^{arctg\sqrt{1+x^2}}\cdot \dfrac{1}{1+(1+x^2)}\cdot \dfrac{1}{2\sqrt{1+x^2}}\cdot (0+2x)=\dfrac{e^{arctg\sqrt{1+x^2}}}{(2+x^2)}\cdot \dfrac{x}{\sqrt{1+x^2}}==\dfrac{x\cdot e^{arctg\sqrt{1+x^2}}}{(2+x^2)\cdot \sqrt{1+x^2}}

rostislavcapsu
rostislavcapsu
4,4(37 оценок)
1м   = 0,001 км 1 г = 0,001 кг 1 см² =   0,01 дм² 1 см³ =   0,001 дм³ 1 л =   0,01 гл 1 ар = 0,01 га 1 га =0,01 км²

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

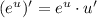Подпишись на наш телеграмм канал

GTP TOP NEWS