vgoidin

29.10.2021 08:06

Геометрия

Есть ответ 👍

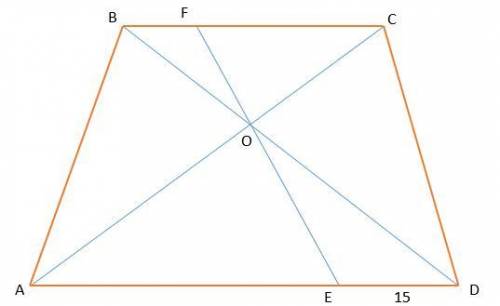
пишите ток без спама. Через точку O, пересекается диагональ трапеции ABCD, прямую, которая пересекает основы AD и BC y точке E и точке F соответственно. Найдите отрезок BF, если DE = 15 см, AO: OC = 3: 2.

271

368

Посмотреть ответы 2

Ответы на вопрос:

kaldyn007

Геометрия

4,4(49 оценок)

10 см

Объяснение:

Дано:

AO:OC=3:2

DЕ=15 см

Найти: BF

Решение.

BC||AD, следовательно ∠OAE=∠FCO, ∠AEO=∠CFO и ∠FOC=∠AOE (как вертикальные). Значит, треугольник AOE и треугольник FOC подобные. Тогда OE:OF=AO:OC=3:2.

Аналогично, ∠OED=∠BFO, ∠FBO=∠ODE и ∠BOF=∠EOD (как вертикальные). Значит, треугольник OED и треугольник BOF подобные. Тогда ED:BF= OE:OF =3:2.

Находим BF

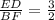
$\frac{ED}{BF}=\frac{3}{2}$

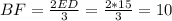
$BF=\frac{2ED}{3}=\frac{2*15}{3}=10$

пишите ток без спама. Через точку O, пересекается диагональ трапеции ABCD, прямую, которая пересекае

Марго215646

Геометрия

4,7(24 оценок)

1) пусть боковая сторона наименьшая и примем ее за х см, тогда сторона основания равна 2x см. периметр треугольника: 2x + 2x = 4x см. составим уравнение

4x = 7

x = 7/4 = 1,75 см.

сторона основания : 2 * 1,75 = 3,5 см.

но треугольник со сторонами 1,75 см; 1,75 см; 3,5 см не существует, поскольку не выполняется неравенство треугольника.

2) пусть сторона основания наименьшая и обозначим ее через х см, тогда боковая сторона равна 2x см. периметр треугольника: x + 2 * 2x = 5x см. составим уравнение:

5x = 7

x = 7/5

x = 1,4 см — сторона основания

боковая сторона: 2 · 1,4 = 2,8 см. и такой треугольник существует.

ответ: 1,4 см; 2,8 см; 2,8 см.

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.