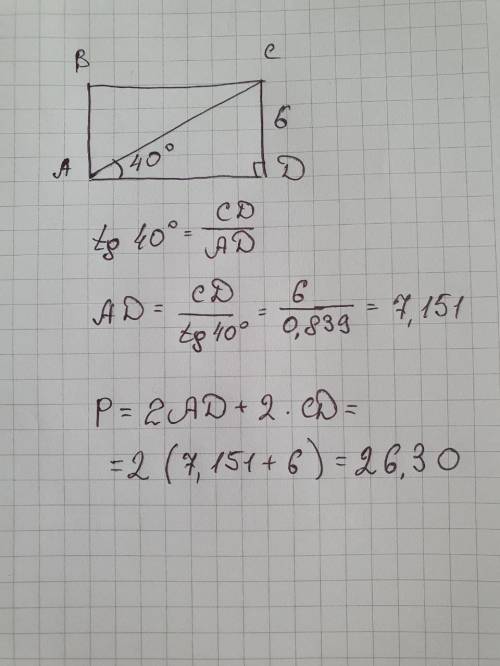50 за грамотное решение. ! 8 класс. в трапеции abcd основание ab в три раза больше основания cd. на основании cd взята точка m так, что mc=2md. n - точка пересечения прямых bm и ac. найдите отношение площади треугольника mnc к площади всей трапеции.

169

378

Посмотреть ответы 2

Ответы на вопрос:

lydmilakucherozh2qq

Геометрия

4,7(79 оценок)

Обозначаем s(cnm) = s , md = m . ⇒ mc = 2*md =2m и cd =md + mc =m +2m =3m , ab =3*cd =3*3m=9m. очевидно: δanb ~ δcnm , причем коэффициент подобия k =ab/ cm =9m/2m =9/2 δanb ~ δcnm ⇒ h₁/ h =k ⇒ h₁=k*h = 9h/2. высота трапеции abcd равна : h = h+h ₁=h +9h/2 =11h/2 . s(cnm) =cm*h/2 =2m*h/2 =m*h ; s(abcd) =(ab +cd)/2 *h =(9m+3m)/2 * 11h/2 = 33m*h ; s(cnm) / s(abcd) =m*h /33m*h =1 : 33 . * * * * * * * другой способ * * * * * * * обозначаем s(cnm) = s , md = m . ⇒ mc = 2*md =2m и cd =md + mc =m +2m =3m , ab =3*cd =3*3m=9m. очевидно: δanb ~ δcnm , причем коэффициент подобия k =an/cn = ab/ cm =9m/2m =9/2 . следовательно s(anb) / s(cnm) = k² ⇒ s(anb) = (81/4)*s . s(anm) / s(cnm) = an / cn = 9/2 ⇒ s(amn) = (9/2) *s .s(bnc) = s(bcm) - s(cnm) = s(amc) -s(cnm) =s(anm) = (9/2) *s .* * * т.е . треугольники bnc и anm равновеликие * * * s(amc) = s(amn) + s(cnm) = (9/2) *s +s =(11/2)*s . s(adm) / s(amc) =md / mc =1/2 ⇒ s(adm) =(1/2)*(11/2) =(11/4)*s. s(abcd) =s(adm) + s(amcb)= s(adm)+s(cnm) + s(anb) +2*s(anm) = (11/4)*s + s +(81/4)*s+ 9*s =(92/4)*s+10*s = 33*s. s / s(abcd) = 1 : 33. p.s. можно было использоватьs(anm) *s(bcn) =s(cnm) * s(anb) ⇔ s²(anm)= 81s/4 *s; s²(anm) =9s/2 и т. д .

никто272

Геометрия

4,7(95 оценок)

26.3

Объяснение:

менша сторона прямокутника дорівнює 6 см, а діагональ утворює з більшою стороною кут 40 градусів. зн

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.