#99-100. Объясните тупому мне, как вынести из под корня/внести под корень, если есть определенное условие (например, а>0 и т.д.). Мне нужно именно ОБЪЯСНЕНИЕ, ведь не понимаю принцип и постоянно теряю или не ставлю "минус" разобрать так каждый пример, соответственно, (НО ГЛАВНОЕ - ПОЯСНЕНИЯ).
Ответы на вопрос:
99) Правило: ![\boxed{\ \sqrt{a^2}=|a|\ \ \ ,\ \ \ \sqrt[2n]{a^{2n}}=|a|\ }](/tpl/images/4529/9104/a373f.png) .
.
При извлечении квадратного корня или корня чётной степени ( 2n - обозначение чётного числа ) из а² (или  ) надо не забыть поставить модуль, ведь сам корень чётной степени может быть только неотрицательным . А модуль любого выражения тоже неотрицателен . Причём, если выражение под модулем неотрицательно, то модуль равен самому этому выражению. Если выражение под модулем отрицательно, то модуль равен этому выражению, взятому с противоположным знаком.
) надо не забыть поставить модуль, ведь сам корень чётной степени может быть только неотрицательным . А модуль любого выражения тоже неотрицателен . Причём, если выражение под модулем неотрицательно, то модуль равен самому этому выражению. Если выражение под модулем отрицательно, то модуль равен этому выражению, взятому с противоположным знаком.
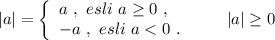
Например, 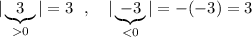 . Как видим, в любом
. Как видим, в любом
случае получаем модуль, равный неотрицательному числу .
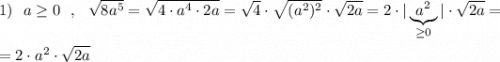
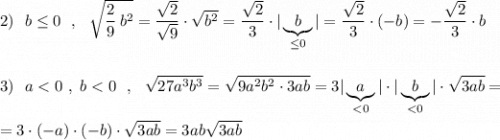
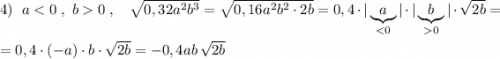
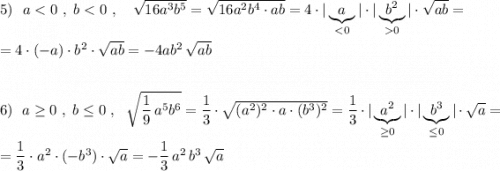
P.S. Обратите внимание, что в 5 примере b<0 , но под модулем записан b² , который несмотря на отрицательное b всё равно будет положительным, и тогда 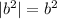 .
.
В 6 примере, так как b≤0 , нечётная степень b тоже будет неположительной, тогда если 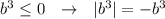 .
.
100) Если 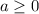 , то
, то ![a=\sqrt{a^2}\ \ ,\ \ a=\sqrt[2n]{a^{2n}}](/tpl/images/4529/9104/decbc.png) .
.
Если 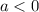 , то
, то ![a=-\sqrt{a^2}\ \ ,\ \ a=-\sqrt[2n]{a^{2n}}](/tpl/images/4529/9104/b5eb6.png) .
.
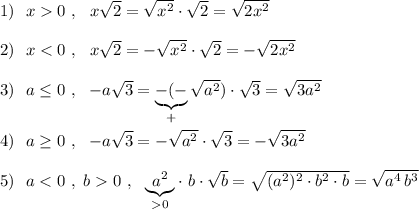

Заметь, что все выражения под знаком квадратного корня или корня чётной степени неотрицательны ! И когда мы внесли под корень множители, получившиеся выражения должны быть неотрицательными .
Например, в 6 примере:
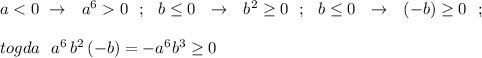
a≤1⇒решений нет; a> 1⇒ 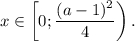
Объяснение:
Левая часть неравенства неотрицательна, поэтому при a≤0 решений нет.
Пусть a>0. Рассмотрим функцию 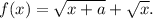 Это возрастающая функция на своей области определения
Это возрастающая функция на своей области определения 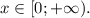
Если ![a\in(0;1],](/tpl/images/4978/0954/d6235.png)
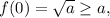 а тогда в силу возрастания f(x)≥a на области определения, поэтому при таких a решений нет.
а тогда в силу возрастания f(x)≥a на области определения, поэтому при таких a решений нет.
Пусть a>1. В этом случае 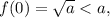 и нам нужно поймать момент, когда f(x) станет равен a. Итак, решаем уравнение
и нам нужно поймать момент, когда f(x) станет равен a. Итак, решаем уравнение 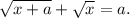
Обозначим 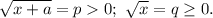 Поскольку p²-q²=a, уравнение равносильно системе
Поскольку p²-q²=a, уравнение равносильно системе 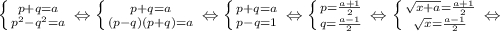
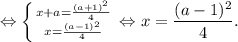 Напомним еще раз, что функция f(x) возрастающая, поэтому слева от найденной точки функция меньше a, справа - больше a. Не забываем и про область определения.
Напомним еще раз, что функция f(x) возрастающая, поэтому слева от найденной точки функция меньше a, справа - больше a. Не забываем и про область определения.
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
Решить тригонометрическое уравнение sin2x+2sinxcosx-3cos2x=0...
 Лейла004426.02.2023 10:16
Лейла004426.02.2023 10:16 -
Втреугольнике авс : ас равно вс равно 10 соs a равно 0,4 найдите ав...
 JiJiMi14.10.2020 07:30
JiJiMi14.10.2020 07:30 -
Арифметическая прогрессия 7,5+9,8+12,1++53,5 объясните откуда они взяли...
 margoskliar03.12.2021 03:55
margoskliar03.12.2021 03:55 -
Решите надо! в правильной четырёхугольной усечённой пирамиде высота равна...
 gabbasovilas24.11.2022 20:13
gabbasovilas24.11.2022 20:13 -
Разложите многочисленны на множетели: x^6-9 ; 2a^4-a^3-2b^2+ab ; a^3x^2+x^2-a^5x-a^2x...
 yulia1468305.04.2020 08:05
yulia1468305.04.2020 08:05 -
Найти все значения, которые принимает функция: f(x) = (3x^2 + x + 1) /...
 Аксинья2113.06.2020 06:02
Аксинья2113.06.2020 06:02 -
Втреугольнике авс : ас равно вс равно 10 соs a равно 0,4 найдите ав...
 kabilet77715.07.2022 03:29
kabilet77715.07.2022 03:29 -
Хозяин овощной лавки купил на оптовом рынке 100кг помидор и заплатил 4000...
 Madwoman1708.10.2021 02:26
Madwoman1708.10.2021 02:26 -
Решите надо. набирая номер телефона абонент забыл последние две цифры и...
 AliceКрошка14.03.2020 00:32
AliceКрошка14.03.2020 00:32 -
Имеет ли смысл выражение: а). квадратный корень из sin 10,2пи б). квадратный...
 КИРА2801200723.03.2023 20:15
КИРА2801200723.03.2023 20:15

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.
