Дан прямоугольный параллелепипед авсda1b1c1d1. найдите двугранный угол b1adb, если известно, что четырехугольник авсd - квадрат, ас= 6, ав1=4 см

244

293

Посмотреть ответы 2

Ответы на вопрос:

95731

Геометрия

4,4(36 оценок)

Рисунок простой, поэтому прямоугольный параллелепипед abcda1b1c1d1 с отрезками ac и ab1 построишь самостоятельно. решение. угол в1ав - линейный угол двугранного угла b1adb (ва перпендикулярно аd т к по условию abcda1b1c1d1 - прямоугольный параллелепипед, в1а перпендикулярно аd по теореме о трех перпендикулярах). т к abcd - квадрат и ас=6, то ав=6/√2.

Angel28648

Геометрия

4,7(60 оценок)

AB₁ = 24,5

CA₁ = 6,5

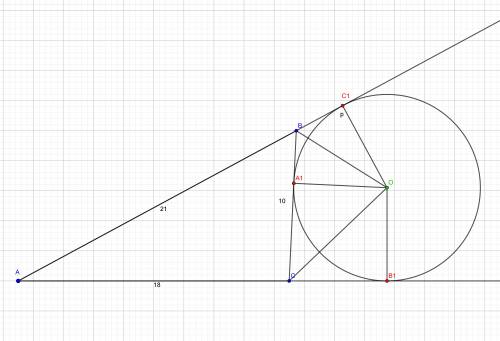
BC₁ = 3,5

Объяснение:

Тогда отрезки касательных от вершины A до точек касания с вневписанной окружностью равны полупериметру треугольника. (Теорема).

AB₁ = 0,5 (21 + 18 + 10) = 24,5

CO и BO - биссектрисы (т.к O - центр)

OB₁ = OA₁ = OC₁ - перпендикуляры (т.к. радиусы к точке касания)

ΔСOA₁ = ΔСOB₁ и ΔBOA₁ = ΔBOC₁ (Хоть по двум сторонам и углу, хоть по двум углам) (если надо конкретно расписать - скажи, я распишу)

СB₁ = AB₁ - AC = 24,5 - 18 = 6,5

СA₁ = СB₁ = 6,5

BC₁ = BA₁ = CB - СA₁ = 10 - 6,5 = 3,5

============

Не забывайте нажать " ", поставить оценку и, если ответ удовлетворил, то выберите его как "Лучший"

Бодрого настроения и добра!

Успехов в учебе!

Вневписанная окружность треугольника ABC касается стороны BC в точке A1, а продолжений сторон AB и A

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.