Регистрация Спросить otvet5GPT
son9a
09.03.2020 14:49
Алгебра
Есть ответ 👍

При каких значениях параметра a неравенство выполняется при любых значениях x. (ax^2+3x+4)/(x^2+2x+2)<5

249
284
Посмотреть ответы 2

Ответы на вопрос:

dinara56437
dinara56437
4,6(100 оценок)

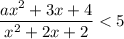
\dfrac{ax^{2} + 3x + 4}{x^{2} + 2x + 2} < 5

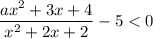
\dfrac{ax^{2} + 3x + 4}{x^{2} + 2x + 2} - 5 < 0

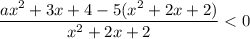
\dfrac{ax^{2} + 3x + 4 - 5(x^{2} + 2x + 2)}{x^{2} + 2x + 2} < 0

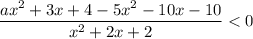
\dfrac{ax^{2} + 3x + 4 - 5x^{2} - 10x - 10}{x^{2} + 2x + 2} < 0

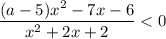
\dfrac{(a - 5)x^{2} - 7x - 6}{x^{2} + 2x + 2} < 0

Неравенство вида 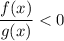\dfrac{f(x)}{g(x)} < 0 равносильно двум системам неравенств:

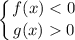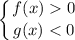
\displaystyle \left \{ {{f(x) < 0} \atop {g(x) 0}} \right. и \displaystyle \left \{ {{f(x) 0} \atop {g(x) < 0}} \right.

Тогда имеем две системы неравенств:

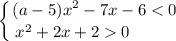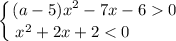
\displaystyle \left \{ {{(a-5)x^{2} - 7x - 6 < 0} \atop {x^{2} + 2x + 2 0 \ \ \ \ \ \ \ \ }} \right. и \displaystyle \left \{ {{(a-5)x^{2} - 7x - 6 0} \atop {x^{2} + 2x + 2 < 0 \ \ \ \ \ \ \ \ }} \right.

Рассмотрим первую систему неравенств:

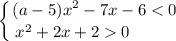
\displaystyle \left \{ {{(a-5)x^{2} - 7x - 6 < 0} \atop {x^{2} + 2x + 2 0 \ \ \ \ \ \ \ \ }} \right.

Решим второе неравенство системы:

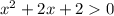
x^{2} + 2x + 2 0

Пересечение с осью абсцисс:

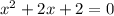
x^{2} + 2x + 2 = 0

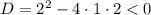
D = 2^{2} - 4 \cdot 1 \cdot 2 < 0

Дискриминант отрицательный, значит график квадратичной функции 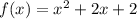f(x) = x^{2} + 2x + 2 находится над осью абсцисс и при любых x больше нуля.

Тогда решением неравенства будет 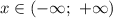x \in (-\infty; \ +\infty)

Рассмотрим первое неравенство системы:

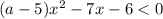
(a-5)x^{2} - 7x - 6 < 0

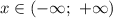Поскольку следует найти значения параметра a, при которых x \in (-\infty; \ +\infty), то для решения системы неравенств нужно, чтобы и данное неравенство имело решение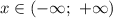 x \in (-\infty; \ +\infty)

Если 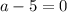a -5 = 0, то есть 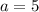a = 5, то имеем линейное неравенство:

-7x - 6 < 0

Решением данного неравенства будет 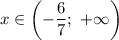x \in \left(-\dfrac{6}{7} ; \ +\infty \right), что не удовлетворяет условию задачи.

Тогда при 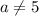a \neq 5 решим неравенство.

Если 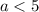a < 5, то имеем параболу с ветвями, направленными вниз, если 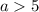a 5, то имеем параболу с ветвями, направленными вверх.

Пересечение с осью абсцисс:

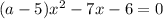
(a-5)x^{2} - 7x - 6 = 0

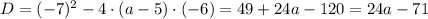
D = (-7)^{2} - 4 \cdot (a - 5) \cdot (-6) = 49 + 24a -120 = 24a - 71

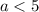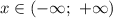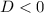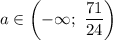
Если a < 5, то данное неравенство будет иметь решение x \in (-\infty; \ +\infty), если D < 0, то есть если 24a - 71 < 0 или a \in \left(-\infty; \ \dfrac{71}{24}\right)

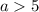Если a 5, то данное неравенство не может иметь решение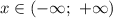 x \in (-\infty; \ +\infty)

Таким образом, если 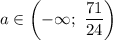a \in \left(-\infty; \ \dfrac{71}{24}\right) имеем решение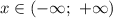 x \in (-\infty; \ +\infty)

Рассмотрим вторую систему неравенств:

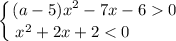
\displaystyle \left \{ {{(a-5)x^{2} - 7x - 6 0} \atop {x^{2} + 2x + 2 < 0 \ \ \ \ \ \ \ \ }} \right.

Решим второе неравенство системы:

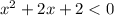
x^{2} + 2x + 2 < 0

Пересечение с осью абсцисс:

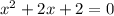
x^{2} + 2x + 2 = 0

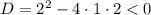
D = 2^{2} - 4 \cdot 1 \cdot 2 < 0

Если дискриминант отрицательный, то квадратичная функция 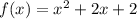f(x) = x^{2} + 2x + 2 никогда не будет меньше нуля.

Тогда решением неравенства будет 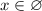x \in \varnothing

Тогда общим решением системы неравенств будет 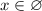x \in \varnothing, независимо от значений параметра a

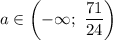
ответ: a \in \left(-\infty; \ \dfrac{71}{24}\right)

Husky333
Husky333
4,8(32 оценок)
5/16 = 0,3125 7/8 = 0,875

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS