Регистрация Спросить otvet5GPT
elizovetadobinda
Есть ответ 👍

И ЛУЧШИЙ ОТВЕТ! ПРЯМ НАДО

109
364
Посмотреть ответы 1

Ответы на вопрос:

EeVoNGuY
EeVoNGuY
4,8(6 оценок)

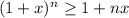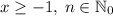Докажем неравенство Бернулли: (1+x)^{n}\geq 1+nx, x\geq -1,\; n\in \mathbb{N}_{0}.

База индукции: 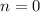n=0 — тут очевидно.

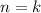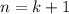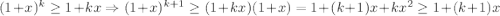Пусть выполняется для некоторого n=k, покажем, что выполняется для n=k+1: (1+x)^k\geq 1+kx \Rightarrow (1+x)^{k+1}\geq (1+kx)(1+x)=1+(k+1)x+kx^2\geq 1+(k+1)x.

Рассмотрим последовательность 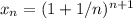x_{n}=(1+1/n)^{n+1} (степень специально на 1 больше — это потребуется при применении неравенства Бернулли)

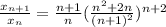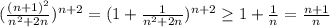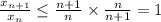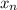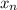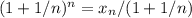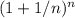\frac{x_{n+1}}{x_{n}}=\frac{n+1}{n}(\frac{n^2+2n}{(n+1)^2})^{n+2}. (\frac{(n+1)^2}{n^2+2n})^{n+2}=(1+\frac{1}{n^2+2n})^{n+2}\geq 1+\frac{1}{n}=\frac{n+1}{n}. Поэтому \frac{x_{n+1}}{x_{n}} \leq \frac{n+1}{n}\times \frac{n}{n+1}=1, значит, x_{n} убывает (монотонно). Понятно, что x_{n} ограничена снизу хотя бы нулем, поэтому имеет предел. Поскольку (1+1/n)^n=x_n/(1+1/n), то (1+1/n) ^n ограничена сверху, причем тем же числом, каким 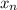x_{n} ограничена снизу.

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Немецкий язык

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS