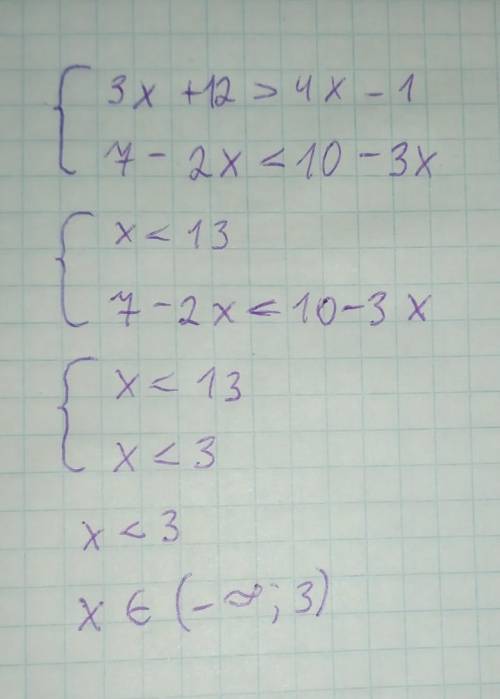Регистрация Спросить otvet5GPT
altyn02
18.08.2020 14:15
Математика
Есть ответ 👍

Исследовать на сходимость ряд: (*знак суммы* в пределах от n=1 до бесконечности) = (2n-1)! /n!

214
270
Посмотреть ответы 2

Ответы на вопрос:

olgap51olga
olgap51olga
4,5(74 оценок)
Отношение следующего члена к предыдущему: a(n+1)/a(n)=[(n+1)! /n! ]^2*[(3n+1)/(3n+4)]*(2n)! /(2n+2)! < < (n+1)^2*1*(2n)! /[(+1)(2n+2)]= =(n+1)^2/[(2n+1)(2n+2)]=(n+1)/[2*(2n+1)]-> 1/4=> сходится.
veronika1217
veronika1217
4,8(19 оценок)

Держи

Надеюсь


Система неравенств решите

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS