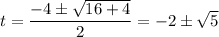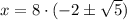Ответы на вопрос:
3sinx + 3cosx=4sinxcosx 3sinx - 4sinxcosx + 3cosx=0 (делим на сosx) 3tgx - 4sinx + 3=0
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
Вынеси общий множитель за скобки 2x - 2y = 2 ...
 clever11323.10.2021 03:59
clever11323.10.2021 03:59 -
Дано квадратное уравнение ^2 − 8 + с = 0. a) При каких значениях параметра...
 supertriom26.12.2020 03:36
supertriom26.12.2020 03:36 -
X=y x+y=3 y=2+x x+y=8 2x-y=0 y=-x...
 alisiababenkov20.09.2021 07:03
alisiababenkov20.09.2021 07:03 -
Велосипедист проехал 40 км, причем , 2 ч он ехал по лесной дороге и 1 ч по...
 ellaakobyan03.06.2021 16:20
ellaakobyan03.06.2021 16:20 -
Составьте уравнение касательных к графику функции x^4+x^2-2, в точках его...
 Ilka1k18.08.2021 08:44
Ilka1k18.08.2021 08:44 -
При каких значениях параметра а уравнение (√х – a)(4x - 9) = 0 имеет единственное...
 vvbybrjnbr09.09.2022 09:34
vvbybrjnbr09.09.2022 09:34 -
Вычислить площадь фигуры, ограниченной линиями у=x²-1; y=0; x=1; x=3...
 fatimo4kkkka22.02.2022 13:25
fatimo4kkkka22.02.2022 13:25 -
Построить график функции y=-3x+5 с построенного графика найти: 1)значение...
 LunaLovegood2822.02.2023 20:45
LunaLovegood2822.02.2023 20:45 -
(sin(7pi/24)cos(pi/24)-cos(7pi/24)sin(pi/24))/(cos(pi/7)cos(4pi/21)-sin(pi/7)sin(4pi/21))...
 kimaleks197728.08.2021 10:19
kimaleks197728.08.2021 10:19 -
Побудувати трикутник за діома кутами і стороно : 6см,110°,30°...
 ruslana050607.03.2023 00:51
ruslana050607.03.2023 00:51

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

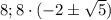
![\left(\dfrac{x+8}{16}\right)^3=\sqrt[3]{x}-1\\ \dfrac{1}{2}\left(\dfrac{1}{2}\cdot \dfrac{x}{8}+\dfrac{1}{2}\right)^3+\dfrac{1}{2}=\sqrt[3]{\dfrac{x}{8}}\\ \left(\dfrac{1}{2}\left(\dfrac{1}{2}\cdot \underbrace{\dfrac{x}{8}}_{t}+\dfrac{1}{2}\right)^3+\dfrac{1}{2}\right)^3=\underbrace{\dfrac{x}{8}}_{t}\\ \left(\dfrac{1}{2}\left(\dfrac{1}{2} t+\dfrac{1}{2}\right)^3+\dfrac{1}{2}\right)^3=t](/tpl/images/4543/3614/34e97.png)
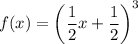 .
.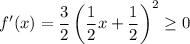 - значит, функция монотонно возрастает.
- значит, функция монотонно возрастает. 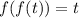 . Но тогда оно равносильно
. Но тогда оно равносильно 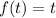 :
: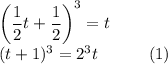
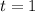 является корнем
является корнем 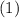 . Тогда
. Тогда 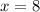 .
. 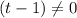 :
: