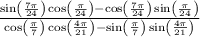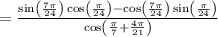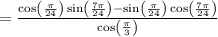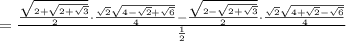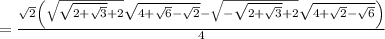(sin(7pi/24)cos(pi/24)-cos(7pi/24)sin(pi/24))/(cos(pi/7)cos(4pi/21)-sin(pi/7)sin(4pi/21))
113
473
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
Решите уравнение: (2x+34)*12=5x/33...
 LeRaDrEeMuRuNdErTaLe26.04.2022 12:10
LeRaDrEeMuRuNdErTaLe26.04.2022 12:10 -
Дана арифметическая прогрессия (an) для которой а6=3 а9=0...
 Ляляляля10919.12.2020 18:01
Ляляляля10919.12.2020 18:01 -
2) 3x(x-4)-6(x^2+2x) преобразуйте в многочлен стандартного вида выражение3)5a(a^2-4a)-8a(a^2-6a)...
 Tishukvasiliy29.06.2020 04:24
Tishukvasiliy29.06.2020 04:24 -
Из полного набора домино извлекают одну костяшку найти вероятность того что...
 nikitos13372813.04.2022 08:03
nikitos13372813.04.2022 08:03 -
Постройте график уравнения -3х+2у=2...
 kall422.02.2021 10:59
kall422.02.2021 10:59 -
Как нужно выполнить данное действие ( 0,2^10*5^10), используя свойства степеней?...
 Артур1505150524.06.2020 16:09
Артур1505150524.06.2020 16:09 -
решить a) (a+4)2 в квадрате б) (x-1) 2 в квадрате в) (x-1) 2 в квадрате ...
 andkrutoi201811.01.2021 23:04
andkrutoi201811.01.2021 23:04 -
Не строя график функции y=0,2x-3 выяснить принадлежит ли графику каждая из...
 BanimPoIP04.06.2021 14:09
BanimPoIP04.06.2021 14:09 -
Найдите площадь боковой поверхности пирамиды, все грани которой наклонены...
 byxanceva6kv203.03.2023 12:35
byxanceva6kv203.03.2023 12:35 -
с 10 номера с решением...
 гулинахабирова03.03.2023 10:01
гулинахабирова03.03.2023 10:01

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.