Регистрация Спросить otvet5GPT
Siyahbeyazask1
01.01.2020 17:20
Математика
Есть ответ 👍

Шарик стоит 4рубля. сколько стоит 5 шариков

227
466
Посмотреть ответы 3

Ответы на вопрос:

hakimov676
hakimov676
4,4(8 оценок)
1шарик 4 рубля 5 шариков-? 4*5=20 рублей стоят 5 шариков
igorkurkin02
igorkurkin02
4,7(71 оценок)
4*5=20
VIDJER
VIDJER
4,6(38 оценок)

Докажем, что пяти достаточно.

Пусть 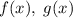f(x),\; g(x) два многочлена четвертой степени, которые совпадают в пяти точках. Тогда f(x)-g(x) является многочленом, имеющим пять корней. Но степень многочлена

Четырех может быть недостаточно: Всего у многочлена четвертой степени пять коэффициентов, значит, пять неизвестных. Четыре уравнения не всегда дают единственное решение.

Можно доказать и более общий результат:

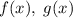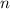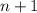Если f(x),\; g(x) — многочлены, степени n, то n+1 — минимальное количество точек, в которых достаточно проверить совпадение многочленов, чтобы доказать их тождественное равенство.

База: для 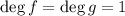\deg f=\deg g=1 все очевидно: по аксиоме требуется две точки для однозначного определения прямой.

Переход: пусть для 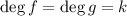\deg f=\deg g=k верно. Докажем истинность для 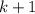k+1. Для этого предположим обратное: достаточно 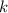k точек. Возьмем различные многочлены 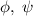\phi,\; \psi степени

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS