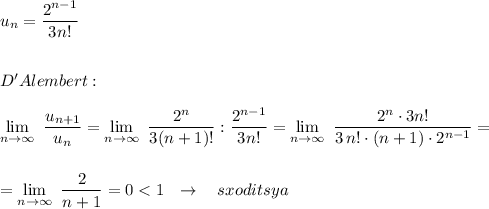Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Математика
-
Решить ! группу из 387 школьников и 63 их педагогов,прибывшие на заключительный...
 vladskills0927.02.2020 10:42
vladskills0927.02.2020 10:42 -
Артур хочет купить машинки ( все они стоят одинаково ).если он купит семь машинок,то...
 asdf203314.09.2021 15:00
asdf203314.09.2021 15:00 -
Найди значения выражений , обозначив порядок действий. 80×5+560: 70×3= 980-(570-170):...
 Иванджелина05.03.2021 08:52
Иванджелина05.03.2021 08:52 -
48 984: 52, 91 375: 43, 243 144: 72, 351 456: 84 в столбик...
 Ylija200215.03.2020 08:18
Ylija200215.03.2020 08:18 -
Аx в х в=ае а х е=е ребусы с числами...
 Duna38329292828220.01.2023 18:51
Duna38329292828220.01.2023 18:51 -
Ширина прямоугольника 2см, длина на 5мм больше найди его периметр...
 danul141401.01.2022 14:59
danul141401.01.2022 14:59 -
Найти cos2a; tg2a; sin2a; ctg2a. если cosa=-3/5...
 alinaalina06024.03.2022 18:09
alinaalina06024.03.2022 18:09 -
На стене в кухне надо заменить плитки на участке прямоугольной формы, длина которого...
 askipolina20.03.2020 22:17
askipolina20.03.2020 22:17 -
Умоляю. решите уровнение. корень из x^2-x-12=x...
 mileenkaaa20.10.2020 01:56
mileenkaaa20.10.2020 01:56 -
2✓3 * sin50sin100+cos50sin10/cos40cos100+sin40cos10...
 gelik757506.08.2020 02:32
gelik757506.08.2020 02:32

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.