Тетяна2401

14.11.2020 03:47

Геометрия

Есть ответ 👍

Точка дотику вписаного кола ділить бічну сторону рівнобедреного трикутника на відрізки 12см і 13см, рахуючи від вершини трикутника. Знайти периметр трикутника !!

174

188

Посмотреть ответы 3

Ответы на вопрос:

Erekcia

Геометрия

4,5(5 оценок)

ответ:Для вирішення цього завдання ми можемо скористатися властивостями вписаного кола в рівнобедрений трикутник.

Перш за все, згідно з властивостями вписаного кола, середина бічної сторони трикутника (дотична точка) є також центром вписаного кола.

Ми можемо позначити радіус цього вписаного кола як "r". За теоремою Піфагора, можемо сказати, що відрізок, який ділить бічну сторону на дві частини, має довжини 12см і 13см, і можемо позначити його як "x".

Тоді інша частина бічної сторони (13см - x) також є відрізком, що ділить бічну сторону на дві частини. За властивостями вписаного кола, ця частина також має довжину 13см.

Таким чином, ми можемо сформулювати рівняння:

x + (13см - x) = 13см

Розкриваємо дужки:

x + 13см - x = 13см

x - x скасовується:

13см = 13см

Отримуємо твердження, яке є тотожнім і завжди істинним. Це означає, що дане рівняння виконується для будь-якого значення "x".

Тепер, щоб знайти периметр трикутника, нам потрібно додати довжини всіх сторін трикутника.

Периметр трикутника = 2x + 13см + 13см

Замінюємо значення x:

Периметр трикутника = 2 * 12см + 13см + 13см

Периметр трикутника = 24см + 13см + 13см

Периметр трикутника = 50см

Отже, периметр трикутника дорівнює 50 см.

Объяснение:

adamka5551p0cigl

Геометрия

4,8(32 оценок)

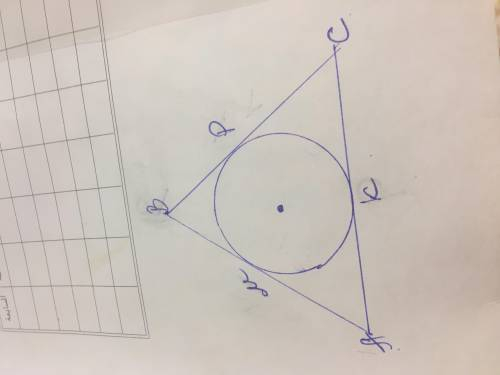
Для решения задачи используем свойства касательных-если из точки вне окружности к окружности проведены касательные,то они равны между собой

МВ=ВР=12 см

АМ=АК=13 см

РС=КС=13 см

Р АВС=(12+13+13)•2=76 см

Объяснение:

Точка дотику вписаного кола ділить бічну сторону рівнобедреного трикутника на відрізки 12см і 13см,

konon707

Геометрия

4,8(90 оценок)

S=a² a1=√s=√75=3√5 a2=√s=√69

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.