26.10.2022 17:13

Есть ответ 👍

У півкруг радіуса 2 см вписана трапеція, периметр якоï 10 см. Знайти площу трапеції, якщо її більша основа діаметр півкруга.

259

277

Посмотреть ответы 3

Ответы на вопрос:

12sa1900

Геометрия

4,4(56 оценок)

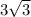
$3\sqrt{3}$

Объяснение:

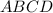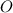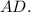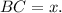Пусть ABCD — данная трапеция, — центр полуокружности и середина основания AD. Тогда OA = OB = OC = OD = 2 см. Пусть верхнее основание BC = x. Опустим из вершин 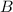и 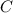высоты на нижнее основание 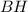и CK.

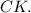
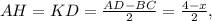
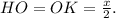$AH = KD = \frac{{AD - BC}}{2} = \frac{{4 - x}}{2},$ $HO = OK = \frac{x}{2}.$ Так как периметр трапеции 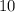см, то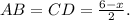 $AB = CD = \frac{{6 - x}}{2}.$

По теореме Пифагора из треугольника 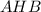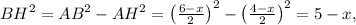AHB $B{H^2} = A{B^2} - A{H^2} = {\left( {\frac{{6 - x}}{2}} \right)^2} - {\left( {\frac{{4 - x}}{2}} \right)^2} = 5 - x,$ а из треугольника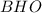 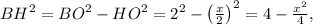BHO $B{H^2} = B{O^2} - H{O^2} = {2^2} - {\left( {\frac{x}{2}} \right)^2} = 4 - \frac{{{x^2}}}{4},$ откуда

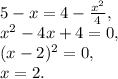
$5 - x = 4 - \frac{{{x^2}}}{4},\\{x^2} - 4x + 4 = 0,\\{(x - 2)^2} = 0,\\x = 2.$

Тогда высота трапеции 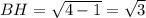$BH = \sqrt {4 - 1} = \sqrt 3$ см, а ее площадь 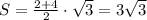$S = \frac{{2 + 4}}{2} \cdot \sqrt 3 = 3\sqrt 3$ см $^{2}.$

SaNur78

Геометрия

4,6(50 оценок)

Відповідь: задача має декілька розв'язків. Один із таких.

У півкруг радіуса 2 см вписана трапеція, периметр якоï 10 см. Знайти площу трапеції, якщо її більша

Sofochka1309

Геометрия

4,4(3 оценок)

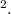
O(4;-3)

(x-4)² + (y+3)² = 4

Объяснение:

А (6;-3) и В (2;-3)

координаты центра

x=(6+2)/2=4

y=(-3-3)/2 = -3

O(4;-3)

R = 2

Общее уравнение окружности

(x-4)² + (y+3)² = 4

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.