rus288

19.12.2021 09:15

Геометрия

Есть ответ 👍

В выпуклом четырехугольнике ABCD известно, что ∠BCD = ∠CDA ⩾ 90◦ . Биссектрисы углов A и B пересекаются в точке M на стороне CD. Докажите, что M — середина CD.

208

225

Посмотреть ответы 2

Ответы на вопрос:

RafSW

Геометрия

4,7(31 оценок)

Доказали, что точка М - середина CD.

Объяснение:

В выпуклом четырехугольнике ABCD известно, что ∠BCD = ∠CDA ⩾ 90◦. Биссектрисы углов A и B пересекаются в точке M на стороне CD. Докажите, что M — середина CD.

Дано: АВСD - выпуклый четырехугольник;

∠BCD = ∠CDA ⩾ 90◦;

ВМ и АМ - биссектрисы ∠В и ∠А соответственно;

М ∈ CD;

Доказать: М - середина CD.

Доказательство:

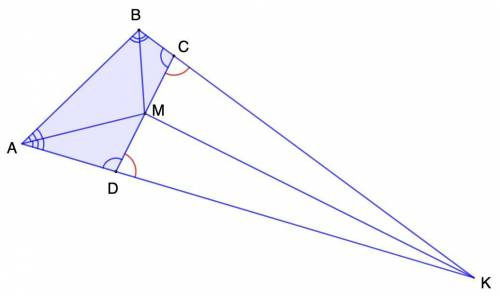
Продолжим стороны ВС и АD до пересечения. Поставим точку К.

Соединим К и М.

1. Рассмотрим ΔАВК.

ВМ и АМ - биссектрисы ∠В и ∠А соответственно. (условие)

Биссектрисы внутренних углов треугольника пересекаются в одной точке.

⇒ КМ - биссектриса ∠К.

2. Рассмотрим ΔDCK.

Сумма смежных углов равна 180°.

⇒ ∠DCK = 180° - ∠BCD

∠CDK = 180° - ∠CDA

∠BCD = ∠CDA (условие)

⇒ ∠DCK = ∠CDK

Если в треугольнике два равных угла, то этот треугольник равнобедренный.

⇒ ΔDCK - равнобедренный.

В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой.

⇒ СМ = MD.

Доказали, что точка М - середина CD.

В выпуклом четырехугольнике ABCD известно, что ∠BCD = ∠CDA ⩾ 90◦ . Биссектрисы углов A и B пересекаю

MalichikSpodezga

Геометрия

4,4(21 оценок)

iэто что значит?

можешь написать это на русском я решу

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.