Алгебра: решить уравнение с параметром

MilkaKamilka5

23.04.2022 13:30

Алгебра

Есть ответ 👍

решить уравнение с параметром

227

492

Посмотреть ответы 2

Ответы на вопрос:

kochergaki2000

Алгебра

4,6(23 оценок)

Если a∈(0;1|, то 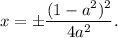$x=\pm \dfrac{(1-a^2)^2}{4a^2}.$ При прочих a решений нет.

Объяснение:

Поскольку 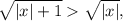$\sqrt{|x|+1} \sqrt{|x|},$ делаем вывод, что a>0. Кроме того, функция 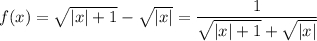$f(x)=\sqrt{|x|+1}-\sqrt{|x|}=\dfrac{1}{\sqrt{|x|+1}+\sqrt{|x|}}$ четная (f(-x)=f(x)) и при x>0 убывающая. Поэтому самое большое значение эта функция достигает при x=0, и это значение равно 1. Поэтому для a можно сделать и такое ограничение: a≤1. Пока мы не знаем, как эти рассуждения нам жить, но хуже точно не будет. Итак, a∈(0;1].

Обозначим:

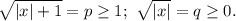$\sqrt{|x|+1}=p\ge 1;\ \sqrt{|x|}=q\ge 0.$ Заметим, что

p²-q²=|x|+1-|x|=1, поэтому для нахождения p и q имеем систему

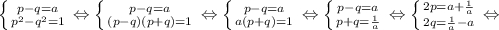
$\left \{ {{p-q=a} \atop {p^2-q^2=1}} \right. \Leftrightarrow \left \{ {{p-q=a} \atop {(p-q)(p+q)=1}} \right.\Leftrightarrow \left \{ {{p-q=a} \atop {a(p+q)=1}} \right. \Leftrightarrow \left \{ {{p-q=a} \atop {p+q=\frac{1}{a}}} \right. \Leftrightarrow \left \{ {{2p=a+\frac{1}{a}} \atop {2q=\frac{1}{a}-a}} \right. \Leftrightarrow$

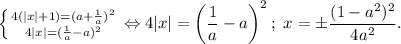
$\left \{ {{4(|x|+1)=(a+\frac{1}{a})^2} \atop {4|x|=(\frac{1}{a}-a)^2}} \right. \Leftrightarrow 4|x|=\left(\dfrac{1}{a}-a\right)^2;\ x=\pm \dfrac{(1-a^2)^2}{4a^2}.$

Кстати, то, что a∈ (0;1), мы использовали при возведении в квадрат второго уравнения системы.

ники2017

Алгебра

4,8(22 оценок)

А)f'(x)=4×5x^4-5×8x^7=20x^4-40x^7 б)f'(x)=(x²-x)'×x+(x²-x)×(x)'=(2x-1)×x+x²-x=2x²-x+x²-x=3x²-2x в)f'(x)=[(x³)'(x+1)-x³(x+1)']/(x+1)²=[3x²(x+1)-x³]/(x+1)²=(2x³+3x²)/(x+1)²

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.