Регистрация Спросить otvet5GPT
roman286
15.06.2023 18:04
Геометрия
Есть ответ 👍

В прямоугольном треугольнике АВС с катетами АС =16 см и ВС = 12 см и гипотенузой АB = 20 см из вершины B проведена биссектриса BD. Найдите длину BD.

218
277
Посмотреть ответы 3

Ответы на вопрос:

lariliv75
lariliv75
4,5(64 оценок)

6√5 см

Объяснение:

используем формулу для нахождения длины биссектрисы через катет и гипотенузу

BD = CB · 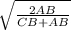\sqrt{\frac{2AB}{CB + AB} } = 12 · \sqrt{\frac{40}{32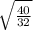} } = 12 · √5/2 = 6√5 см


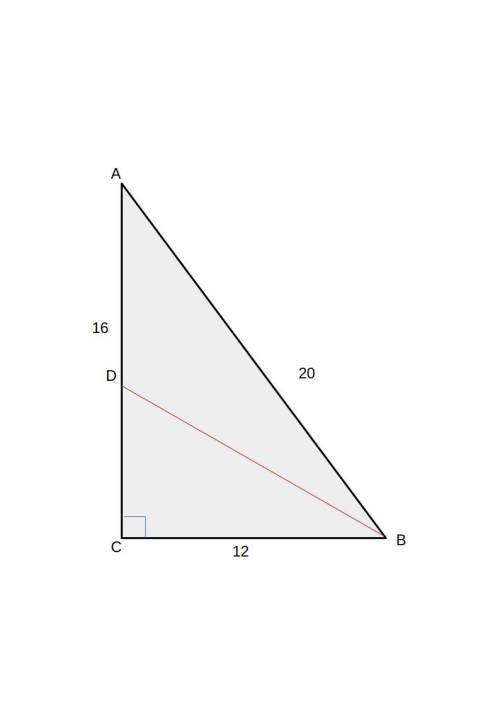
В прямоугольном треугольнике АВС с катетами АС =16 см и ВС = 12 см и гипотенузой АB = 20 см из верши
53490
53490
4,8(58 оценок)

Каждая точка биссектрисы равноудалена от сторон угла, DC=DC1

Площади треугольников с равными высотами относятся как основания.

Треугольники ABD и DBC имеют общую высоту из вершины B и равные высоты из вершины D.

SABD/SDBC =AD/DC =AB/BC

Доказали теорему о биссектрисе в случае прямоугольного треугольника.

Биссектриса делит сторону треугольника в отношении прилежащих сторон.

AD/DC =AB/BC =20/12 =5/3

DC =3/8 AC =6

DBC, т Пифагора

BD =√(BC^2 +DC^2) =6√5 (см)

Или

cosB =BC/AB =3/5

cos(B/2) =√((1+cosB)/2) =√(4/5) =2/√5 (B/2 <90)

BD =BC/cos(B/2) =6√5 (см)


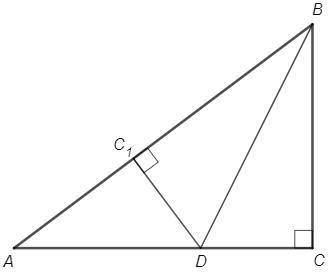
В прямоугольном треугольнике АВС с катетами АС =16 см и ВС = 12 см и гипотенузой АB = 20 см из верши
sestrichkitv
sestrichkitv
4,6(34 оценок)

Вписанный окружность делает четырехугольник симметричным. Одна сторона равна другому.

AD = DC, AB = BC.

Периметр (P) равен сумме всех сторон четырехугольника:

P = AD+DC+AB+BC.

Итак

p = 17 \times 2 + 11 \times 2 = 56

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Геометрия

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS