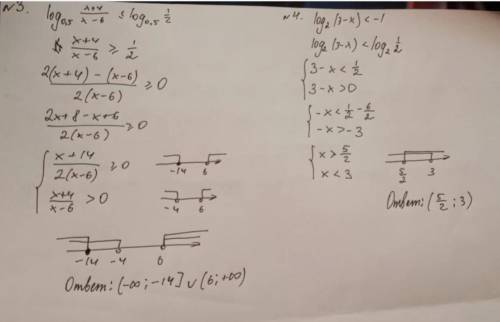Ответы на вопрос:
Решение.
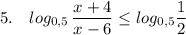
ОДЗ: выражение под знаком log строго больше 0 ,
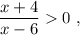 знаки: (-4) - - - - - (6)
знаки: (-4) - - - - - (6) 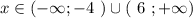
Основание логарифма 0<0,5<1 , поэтому это убывающая функция, и знак между аргументами логарифмической функции будет противоположным .
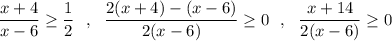
знаки: [-14] - - - - (6) ![x\in (-\infty ;-14\, ]\cup (\ 6\ ;+\infty )](/tpl/images/4906/5028/6865a.png)
C учётом ОДЗ ответ: ![x\in (-\infty ;-14\, ]\cup (\ 6\ ;+\infty )](/tpl/images/4906/5028/6865a.png) .
.
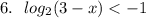
ОДЗ: 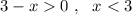
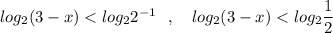
Логарифмическая функция с основанием 2>1 возрастающая, поэтому знак между аргументами логарифмической функции будет таким же .
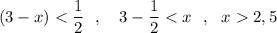
Учтём ОДЗ: 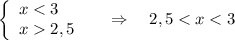
ответ: 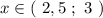 .
.
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
Два икс плюс 4 минус под квадратным корнем икс плюс два равно пятнадцати решить...
 Cill10922.06.2021 11:54
Cill10922.06.2021 11:54 -
2х+4 минус квадратный корень из х+2 равно 15...
 jenjenle12.03.2023 16:58
jenjenle12.03.2023 16:58 -
(16-х^2)/10x=0 нужно решить пример по (здесь дробь)...
 Shkolnik22800713.03.2022 13:48
Shkolnik22800713.03.2022 13:48 -
Kak pisat naprimer 5 v kvadrate ne mogo kvadrat postavit...
 YourMango05.03.2021 17:35
YourMango05.03.2021 17:35 -
Сколько раз в течение суток часовая и минутная стрелки образуют угол 120°? а) 44;...
 Cuba12513.02.2023 18:37
Cuba12513.02.2023 18:37 -
Если взять слово «ромашка», то из букв этого слова можно составить другие слова,...
 feroprosto17.09.2022 11:28
feroprosto17.09.2022 11:28 -
Красивых учеников в классе всего 22, а умных 18.всего в классе 30 учеников и каждый...
 yuliya9103.02.2020 18:44
yuliya9103.02.2020 18:44 -
Бросаю две монеты.какова вероятность того,что: 1)выпадут две решки. 2)выпадут орёл...
 ikol291223.05.2021 05:53
ikol291223.05.2021 05:53 -
Мышка,лягушка,зайчик,лисичка и волчонок построили домики разной формы: треугольный,квадратный,круглый,прямоугольный...
 555сармат55521.07.2022 16:32
555сармат55521.07.2022 16:32 -
Выразите из формулы q=cm(t1-t2) переменную t1...
 mirapax1997ozb3lk14.03.2020 04:06
mirapax1997ozb3lk14.03.2020 04:06

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.