ifrut52

26.02.2020 19:34

Геометрия

Есть ответ 👍

Зовнішній кут при вершині С трикутника АВС дорівнює 130°, а внутрішній кут при вершині В - 60°. Укажіть найбільшу сторону трикутника

146

230

Посмотреть ответы 2

Ответы на вопрос:

flak202

Геометрия

4,6(29 оценок)

ВС - самая большая сторона

Объяснение:

∠С=180°-130°=50° - по свойству развернутого угла.

По свойству сумм угла треугольника:

∠А=180°-∠С-∠B.

∠А=180°-50°-60°.

∠А=70° - этот угол лежит напротив стороны ВС. Этот угол наибольший. Так как напротив большего угла лежит большая сторона. Значит ВС - самая большая сторона.

kolya0125

Геометрия

4,8(7 оценок)

Дано:

Равнобедренная трапеция.

h (трапеции) = 7,5 ед.

Меньшее основание = 2 ед.

Угол при основании = 45°.

Найти:

Большее основание - ?

Решение:

Обозначим данную равнобедренную трапецию буквами A, B, C и D так, что AB - меньшее основание, CD - большее основание, AD и BC - боковые стороны, угол при основании, равный 45° - ∠C, AP - высота.

Так как трапеция ABCD - равнобедренная ⇒ ∠D = ∠C = 45°.

Проведём ещё одну высоту из вершины B к большему основанию трапеции BM так, что AP = BM = 7,5 ед.

Образовалось два прямоугольных треугольника - ADP и BCM. Они равны (их равенство можно доказать по всем признакам равенства прямоугольных треугольников, исходя из того, что трапеция ABCD - равнобедренная).

Сумма острых углов прямоугольного треугольника равна 90°.

⇒ ∠DAP = ∠CBM = 90° - 45° = 45°.

Значит, ΔADP и ΔBCM - равнобедренные.

⇒ AP = DP = BM = MC = 7,5 ед.

Так как AP и BM - высоты и ABCD - равнобедренная трапеция

⇒ AB = PM = 2 ед.

По рисунку можно увидеть, что: CD = DP + PM + MC.

⇒ CD = 7,5 + 2 + 7,5 = 15 + 2 = 17 ед.

ответ: 17 ед.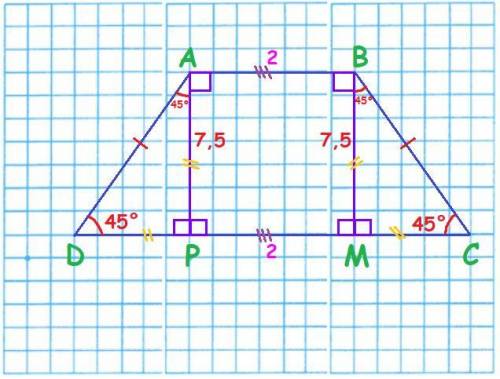
В равнобедренной трапеции высота равна 7, 5, меньшее основание равно 2, и угол при основании равен 4

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.