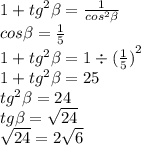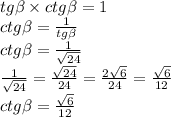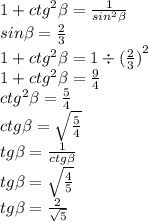Ответы на вопрос:
Найдем радиус основания. по т. пифагора квадрат радиуса=169-144=25 см в квадрате. радиус=5 диагональное сечение - равнобедренный треугольник с основанием=5*2=10 найдем площадь 1/2*12*10=60 см в квадрате
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Геометрия
-
Площадь ромба равна 27 см (в квадрате), одна из диагоналей равна 9 см, надо...
 Виктория8987343694026.03.2023 05:02
Виктория8987343694026.03.2023 05:02 -
Вугле авс проведена биссетриса bd, угол а=75 градусов, кгол с=35 градусам...
 mrfotuna1416.09.2020 01:47
mrfotuna1416.09.2020 01:47 -
Треугольник авс прямоугольный, где угол с равен 90°. проведены биссектрисы...
 Лика150827.12.2022 10:09
Лика150827.12.2022 10:09 -
Площадь квадрата, описанного около окружности, равна 48 см в квадрате. найдите...
 dushka30507029.05.2022 06:00
dushka30507029.05.2022 06:00 -
Что общего у новой зеландии,и у новой гвинеи...
 kata19872221.05.2020 17:03
kata19872221.05.2020 17:03 -
Периметр треугольника равен 56 см, а одна из его сторон больше другой на 6....
 Ya1246799007605.04.2021 11:05
Ya1246799007605.04.2021 11:05 -
Дан треугольник abc, средние линии которого равны 3 см, 6 см и 7 см. определите...
 likaKiss125.03.2023 16:28
likaKiss125.03.2023 16:28 -
Перпендикуляр, проведений через середину бічної сторони рівнобедреного трикутника,...
 Asig16.03.2020 17:49
Asig16.03.2020 17:49 -
Средняя линия трапеции равна 22 см. одно из её оснований на 8 см больше другого....
 Enotlk133724.07.2020 21:37
Enotlk133724.07.2020 21:37 -
Докажите, что для любого угла α из промежутка 0º α 90º справедливы равенства...
 Лера1501200312.08.2020 05:14
Лера1501200312.08.2020 05:14

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.