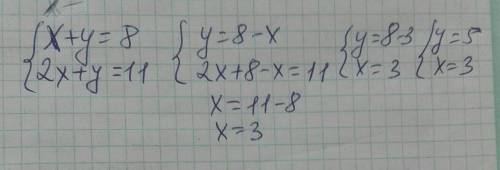Определи, при каком минимальном значении параметра a уравнение 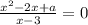 имеет единственный корень.
имеет единственный корень.
215
457
Ответы на вопрос:
a = 1
Объяснение:
Дано уравнение
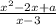 = 0
= 0
Найдём значение параметра a, при котором уравнение имеет единственный корень
Наложим условие, что x ≠ 3 и опустим знаменатель
x² - 2x + a = 0
Для того, чтобы у уравнения был единственный корень, необходимо и достаточно, чтобы дискриминант уравнения равнялся нулю
D = 2² - 4a = 0
4 - 4a = 0
4 = 4a
a = 1
Подставим это значение в уравнение
x² - 2x + 1 = 0
(x - 1)² = 0
x = 1
Это не противоречит условию, наложенному на знаменатель, значит a = 1
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
Решите уравнение 5x^2 − 18x − 23 = (x+1)^2....
 shhfxecbhawc03.04.2020 15:17
shhfxecbhawc03.04.2020 15:17 -
Скоростной электропоезд следуя из города а в город в в первый час проехал 40%,...
 Superfoxygirl11222.03.2023 19:29
Superfoxygirl11222.03.2023 19:29 -
Сократите дробь 1) ax-ay-3x+3y a^2-9 2) (5x-10y)^2 2y-x...
 chcuvivhcyxu27.04.2023 07:10
chcuvivhcyxu27.04.2023 07:10 -
Вычислите координаты точек пересечения параболы и прямой y=x^2-5x y=x+16...
 evelinkazelenyak20.11.2021 14:49
evelinkazelenyak20.11.2021 14:49 -
Нужно решить , : для облицовки стены, имеющей форму прямоугольника со сторонами...
 Александра03030720.04.2021 20:34
Александра03030720.04.2021 20:34 -
Решить неравенство: 2х^2-3х+1 0 я знаю,что если я прировняю все к нулю,то d=1.не...
 sashok003103.11.2020 05:18
sashok003103.11.2020 05:18 -
1)8x²+21x-9=0 2)14x²-19-3=0 3)9x²-30x+25=0 4)5x²-4x=0 5)x²-5=x/2+2,5 6)x²+11x+20=0...
 kashalotic2024.06.2022 16:18
kashalotic2024.06.2022 16:18 -
Высота вн параллелограмма абсд дешит его сторону ад на отрезки ан=5 и нд=28....
 tasn23.05.2022 04:53
tasn23.05.2022 04:53 -
Сократить дробь. x²+3x-10= x-2 x-2. =...
 kiriukhina200717.04.2023 11:03
kiriukhina200717.04.2023 11:03 -
Найдите расстояние от точки пересечения графиков функций до оси ox....
 Sehunjungkook02.12.2020 20:51
Sehunjungkook02.12.2020 20:51

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.