aldynsaioorzhak1

18.08.2021 13:49

Алгебра

Есть ответ 👍

При каких значениях параметр а значение интеграла максимален?

286

410

Посмотреть ответы 2

Ответы на вопрос:

дитус

Алгебра

4,6(31 оценок)

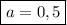
$\boxed{a = 0,5}$

Объяснение:

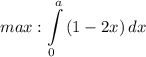
$max: \displaystyle \int\limits^a_0 {(1 - 2x)} \, dx$

Введем функцию: 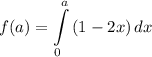$f(a) = \displaystyle \int\limits^a_0 {(1 - 2x)} \, dx$

Неопределенный интеграл:

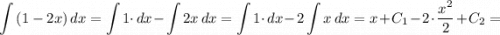
$\displaystyle \int {(1 - 2x)} \, dx = \displaystyle \int {1 \cdot} \, dx - \displaystyle \int { 2x} \, dx = \displaystyle \int {1 \cdot} \, dx - \displaystyle 2 \int {x} \, dx = x + C_{1} - 2 \cdot \dfrac{x^{2}}{2} + C_{2}=$

$= x - x^{2} + C$

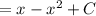
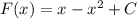$F(x) = x - x^{2} + C$ - первообразная для функции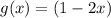 g(x) = (1 - 2x)

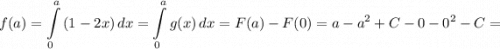
$f(a) = \displaystyle \int\limits^a_0 {(1 - 2x)} \, dx = \displaystyle \int\limits^a_0 {g(x)} \, dx = F(a) - F(0) = a - a^{2} + C - 0 - 0^{2} - C =$

$= a - a^{2}$

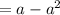
Найдем максимум функции 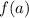f(a) :

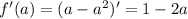
$f'(a) = (a - a^{2})' = 1 - 2a$

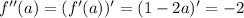
f''(a) = (f'(a))' = (1 - 2a)' = -2

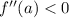f''(a) < 0 следовательно функция 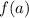f(a) имеет максимум

(при 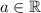$a \in \mathbb R$ )

f'(a) = 0

1 - 2a = 0

2a = 1|:2

a = 0,5

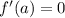
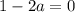
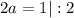
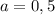
То есть максимум 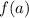f(a) при a = 0,5

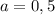
Условие:

При каком значении a значение интеграла 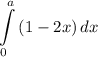$\displaystyle \int\limits^a_0 {(1 - 2x)} \, dx$ максимально?

Ключевые слова:

Интегралы, определенный интеграл, интеграл с параметром, экстремумы функции, максимум функции

lusindrastsr

Алгебра

4,7(100 оценок)

3ху(у-х)=(х^3-3х^2у+3ху^2-у^3)-х^3+у^3 (раскрыли по формуле куб разности) 3ху^2 -3х^2у =3ху^2 -3х^2у (раскрыли скобки в левой части, в правой раскрыли скобки и преобразовали) 0=0 торжество доказано.

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.