Алгебра: за ответ решите a)1+cos α - sin α б)1-sin α - cos α α—это альфа

kabdushevaaynash

08.12.2021 06:07

Алгебра

Есть ответ 👍

за ответ решите a)1+cos α - sin α

б)1-sin α - cos α

α—это альфа

261

467

Посмотреть ответы 2

Ответы на вопрос:

Malinka961

Алгебра

4,5(12 оценок)

Формулы. $1+cosx=2cos^2\dfrac{x}{2}\ \ ,\ \ 1-cosx=2sin^2\dfrac{x}{2}$ ,

$cosx-cosy=-2sin\dfrac{x+y}{2}\cdot sin\dfrac{x-y}{2}\ \ ,\ \ sinx-siny=2sin\dfrac{x-y}{2}\cdot cos\dfrac{x+y}{2}$ .

$a)\ \ 1+cosa-sina=2cos^2\dfrac{a}{2}-2\, sin\dfrac{a}{2}\cdot cos\dfrac{a}{2}=2cos\dfrac{a}{2}\cdot \Big(cos\dfrac{a}{2}-sin\dfrac{a}{2}\Big)==2cos\dfrac{a}{2}\cdot \Big(cos\dfrac{a}{2}-cos(\dfrac{\pi}{2}-\dfrac{a}{2})\Big)=2cos\dfrac{a}{2}\cdot 2\cdot sin\dfrac{\pi }{4}\cdot sin\Big(\dfrac{\pi}{4}-\dfrac{a}{2}\Big)==2\sqrt2cos\dfrac{a}{2}\cdot sin\Big(\dfrac{\pi}{4}-\dfrac{a}{2}\Big)$

$b)\ \ 1-cosa-sina=2sin^2\dfrac{a}{2}-2\, sin\dfrac{a}{2}\cdot cos\dfrac{a}{2}=2sin\dfrac{a}{2}\cdot \Big(sin\dfrac{a}{2}-cos\dfrac{a}{2}\Big)==2sin\dfrac{a}{2}\cdot \Big(sin\dfrac{a}{2}-sin(\dfrac{\pi}{2}-\dfrac{a}{2})\Big)=2sin\dfrac{a}{2}\cdot 2\cdot cos\dfrac{\pi }{4}\cdot sin\Big(\dfrac{a}{2}-\dfrac{\pi}{4}\Big)==2\sqrt2sin\dfrac{a}{2}\cdot sin\Big(\dfrac{a}{2}-\dfrac{\pi}{4}\Big)$

katyaibadova

Алгебра

4,4(40 оценок)

решение на фотографии

Для каждого выражения из левого столбца подберите ему тождественно равное в правом

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.
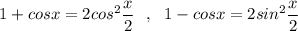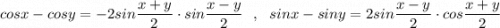