Регистрация Спросить otvet5GPT
tagirok4525
14.02.2022 23:20
Алгебра
Есть ответ 👍

1.8-3x=-5x-12
2.5x-x^2=0
3.(x-4)(x+7)=0
4.25-x^2=0

111
191
Посмотреть ответы 2

Ответы на вопрос:

edikmarik
edikmarik
4,6(34 оценок)

Здесь всё достаточно просто ,нужно было только вспомнить некоторые формулы ,и как решаются квадратные уравнения)


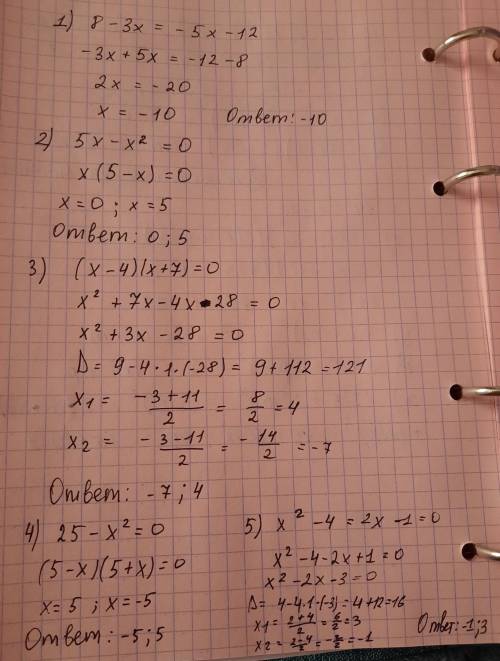
1.8-3x=-5x-12 2.5x-x^2=0 3.(x-4)(x+7)=0 4.25-x^2=0
lissrrtt
lissrrtt
4,5(97 оценок)
Теорема виета  для    квадратного уравнения. сумма корней квадратного уравнения  x2+px+q=0  равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену: x1+x2=-p;   x1∙x2=q.   найти корни квадратного уравнения, используя теорему виета. пример 1) x2-x-30=0.  это квадратное уравнение  (  x2+px+q=0), второй коэффициент   p=-1, а свободный член  q=-30.  сначала убедимся, что данное уравнение имеет корни, и что корни (если они есть) будут выражаться целыми числами. для этого достаточно, чтобы дискриминант был полным квадратом целого числа. находим дискриминант  d=b2— 4ac=(-1)2-4∙1∙(-30)=1+120=121=112. теперь по теореме виета сумма корней должна быть равна второму коэффициенту, взятому с противоположным знаком, т.е. (-p), а произведение равно свободному члену, т.е. (q). тогда: x1+x2=1; x1∙x2=-30.  нам надо подобрать такие два числа, чтобы их произведение было равно  -30, а сумма –  единице. это числа  -5  и  6.  ответ: -5; 6. пример 2) x2+6x+8=0.  имеем квадратное уравнение со вторым коэффициентом  р=6  и свободным членом  q=8. убедимся, что есть целочисленные корни. найдем дискриминант  d1, так как второй коэффициент – четное число.  d1=32-1∙8=9-8=1=12. дискриминант d1  является полным квадратом числа  1, значит, корни данного уравнения являются целыми числами. подберем корни по теореме виета: сумма корней равна  –р=-6, а произведение корней равно  q=8. это числа  -4  и  -2. на самом деле: -4-2=-6=-р; -4∙(-2)=8=q.  ответ: -4; -2. пример 3) x2+2x-4=0. в этом квадратном уравнении второй коэффициент  р=2, а свободный член  q=-4. найдем дискриминант  d1, так как второй коэффициент – четное число.  d1=12-1∙(-4)=1+4=5.  дискриминант не является полным квадратом числа, поэтому, делаем  вывод:   корни данного уравнения не являются целыми числами и найти их по теореме виета нельзя.  значит, решим данное уравнение, как обычно, по формулам (в данном случае по формулам  для частного случая с четным вторым коэффициентом). получаем:  пример 4).  составьте квадратное уравнение по его корням, если  x1=-7, x2=4. решение.  искомое уравнение запишется в виде:   x2+px+q=0, причем, на основании теоремы виета  –p=x1+x2=-7+4=-3  → p=3;   q=x1∙x2=-7∙4=-28. тогда уравнение примет вид:   x2+3x-28=0. пример 5).  составьте квадратное уравнение по его корням, если:  ii. теорема виета  для  полного  квадратного уравнения  ax2+bx+c=0. сумма корней равна минус  b, деленному на  а, произведение корней равно  с, деленному на  а: x1+x2=-b/a;   x1∙x2=c/a. пример 6).  найти сумму корней квадратного уравнения  2x2-7x-11=0. решение. убеждаемся, что данное уравнение будет иметь корни. для этого достаточно составить выражение для дискриминанта, и, не вычисляя его, просто убедиться, что дискриминант больше нуля.  d=72-4∙2∙(-11)> 0. а теперь воспользуемся  теоремой  виета  для полных квадратных уравнений. x1+x2=-b: a=- (-7): 2=3,5. пример 7). найдите произведение корней квадратного уравнения  3x2+8x-21=0. решение. найдем дискриминант  d1, так как второй коэффициент (8) является четным числом.  d1=42-3∙(-21)=16+63=79> 0. квадратное уравнение имеет  2  корня, по теореме виета произведение корней  x1∙x2=c: a=-21: 3=-7.      

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS