Регистрация Спросить otvet5GPT
Nozzer4K
09.06.2023 17:06
Алгебра
Есть ответ 👍

В параллелограмме ABCD известны координаты трёх его вершин: A (4, −4), B (3, −1) и C (5, −3). Пусть K− точка пересечения диагоналей параллелограмма ABCD. При каком значении параметра t вектор a = (t, 2) имеет c вектором AK угол 45 градусов? Необходимо с решением

182
445
Посмотреть ответы 2

Ответы на вопрос:

tkalenko03
tkalenko03
4,5(76 оценок)

Диагонали параллелограмма в точке пересечения делятся пополам.

Находим координаты точки К как середины АС

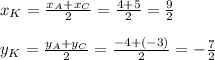
x_{K}=\frac{x_{A}+x_{C}}{2} =\frac{4+5}{2}=\frac{9}{2} y_{K}=\frac{y_{A}+y_{C}}{2} =\frac{-4+(-3)}{2}=-\frac{7}{2}

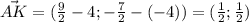
\vec{AK}=(\frac{9}{2}-4;-\frac{7}{2}-(-4))=(\frac{1}{2}; \frac{1}{2})

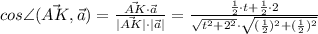
cos\angle(\vec{AK}, \vec{a})=\frac{\vec{AK}\cdot \vec{a}}{|\vec{AK}|\cdot |\vec{a}|}=\frac{\frac{1}{2}\cdot t+\frac{1}{2}\cdot 2}{\sqrt{t^2+2^2}\cdot\sqrt{(\frac{1}{2})^2+(\frac{1}{2})^2}}

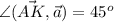
\angle(\vec{AK}, \vec{a})=45^{o}

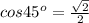
cos45^{o}=\frac{\sqrt{2}}{2}

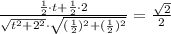
\frac{\frac{1}{2}\cdot t+\frac{1}{2}\cdot 2}{\sqrt{t^2+2^2}\cdot\sqrt{(\frac{1}{2})^2+(\frac{1}{2})^2}}=\frac{\sqrt{2}}{2}

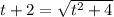
t+2=\sqrt{t^2+4}

Возводим в квадрат

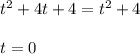
t^2+4t+4=t^2+4t=0

Проверка:

0+2=√(0^2+4)-  верно

ответ. t=0

lineage216
lineage216
4,7(100 оценок)
6x^2=7-x 6x^2+x-7=0 x1=-7/6 x2=1

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS