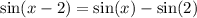Регистрация Спросить otvet5GPT
равиль7777777
27.06.2020 20:00
Алгебра
Есть ответ 👍

решить \sin(x - 2) = \sin(x) - \sin(2)
найти кол во корней на промежутке
[0;2п]

268
326
Посмотреть ответы 2

Ответы на вопрос:

оля27102000
оля27102000
4,5(69 оценок)

(см. объяснение)

Объяснение:

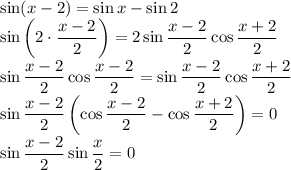
\sin(x-2)=\sin x-\sin2\\\sin\left(2\cdot\dfrac{x-2}{2}\right)=2\sin\dfrac{x-2}{2}\cos\dfrac{x+2}{2}\\\sin\dfrac{x-2}{2}\cos\dfrac{x-2}{2}=\sin\dfrac{x-2}{2}\cos\dfrac{x+2}{2}\\\sin\dfrac{x-2}{2}\left(\cos\dfrac{x-2}{2}-\cos\dfrac{x+2}{2}\right)=0\\\sin\dfrac{x-2}{2}\sin\dfrac{x}{2}=0

Произведение равно 0, когда хотя бы 1 из его множителей равен 0, а другие при этом не теряют смысла.

Тогда:

\left[\begin{array}{c}\sin\dfrac{x-2}{2}=0sin\dfrac{x}{2}=0\end{array}\right;

Для первой строки совокупности:

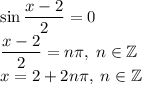
\sin\dfrac{x-2}{2}=0\\\dfrac{x-2}{2}=n\pi,\;n\in\mathbb{Z}\\x=2+2n\pi,\;n\in\mathbb{Z}

Для второй строки совокупности:

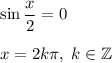
\sin\dfrac{x}{2}=0x=2k\pi,\;k\in\mathbb{Z}

Итого получили, что ответ:

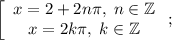
\left[\begin{array}{c}x=2+2n\pi,\;n\in\mathbb{Z}\\x=2k\pi,\;k\in \mathbb{Z}\end{array}\right;

Найдем теперь количество корней уравнения на промежутке [0;\;2\pi].

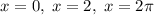Это: x=0,\;x=2,\;x=2\pi.

Тогда ответом будет число 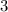3.

Задание выполнено!

Ketti08
Ketti08
4,6(41 оценок)

для начала, найдем путь, который пройдет точка за 2 секунды. для этого подставляем значение t=2 в уравнение.

4*2-1/2+1=7.5

теперь найдем скорость

v=s/t

v=7.5/2=3.75

ответ: v=3.75

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS