OkumRin

05.06.2023 15:04

Есть ответ 👍

Установить, как расположена точка А(1; -2) относительно окружности x^2+y^2 = 1 - внутри, вне или на контуре. Указание: для решения воспользоваться свойством расположения точки М1(х1; y1) и окружности (школьный курс геометрии 8-9 класс).

142

304

Посмотреть ответы 2

Ответы на вопрос:

мама1035

Математика

4,5(13 оценок)

точка A(1;-2) расположена вне окружности

Пошаговое объяснение:

Решим задание через определение степени точки относительно окружности

Степенью точки относительно данной окружности называется разность

${ d^{2}-R^{2}} ,$

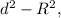
d — расстояние от точки до центра окружности,

R — радиус окружности.

Точки имеют следуюющие степени в зависимости от расположения:

- вне окружности - положительную,

- внутри окружности - отрицательную,

- на окружности - нулевую.

Общее уравнение окружности задается уравнением

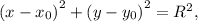
$\left(x-x_{0}\right)^{2}+\left(y-y_{0}\right)^{2}=R^{2},$

где (х0, у0) - координаты центра окружности

R - ее радиус.

В нашем случае:

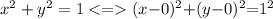
$x^2+y^2 = 1 < = (x{ - }0) {}^{2}{ +} (y{ -} 0) {}^{2}{ = } {1}^{2}$

Следовательно,

радиус окружности R = 1;

центр окружности O = О(0; 0)

Теперь вычислим степень точки A(1;-2) относительно этой окружности:

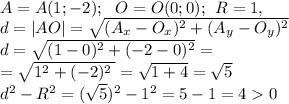
$A = A(1;-2); \: \: \: O =O(0;0); \: \: { R = 1} , \\ d=|AO|=\sqrt{(A_x-O_x)^2+(A_y-O_y)^2} \\ d = \sqrt{(1 - 0) {}^{2} + ( - 2 - 0) {}^{2} } = \\ = \sqrt{ {1}^{2} + ( - 2) {}^{2} \: } = \sqrt{1 + 4} = \sqrt{5} \\ {d}^{2} - {R}^{2} = ( \sqrt{5} )^{2} - {1}^{2} = 5 - 1 = 4 0$

Итак мы выяснили, что d² - R² > 0 =>

=> точка A(1;-2) расположена вне окружности.

saidrasulov15

Математика

4,6(78 оценок)

6+8=14 280: 14=20 ответ: 20

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.