lika771

21.09.2022 23:45

Есть ответ 👍

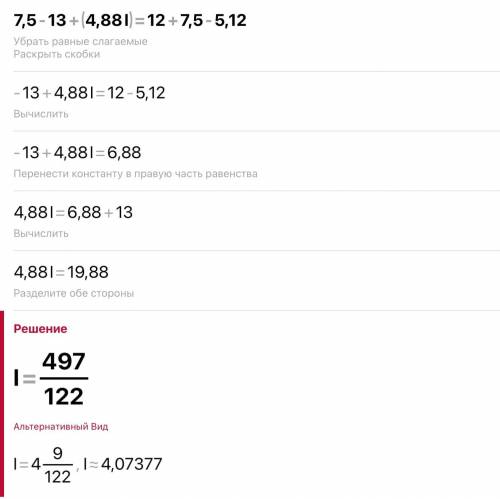
Уравнение прямой проходящей через точки. А(1; 2) и B(-1; 3) имеет вид: Выберите один ответ:
x-2y+3=0
x+2y-5=0
x+y-2=0
x-2y-5=0

252

368

Посмотреть ответы 3

Ответы на вопрос:

EkaterinaZeyb

Алгебра

4,4(77 оценок)

ответ: б)

Объяснение:

Во вложении

Уравнение прямой проходящей через точки. А(1; 2) и B(-1; 3) имеет вид: Выберите один ответ: x-2y+3=0

Łųçů

Алгебра

4,6(3 оценок)

х + 2у - 5=0

Объяснение:

Есть 2 варианта решения:

1) Подстановка значений в варианты ответов:

Подставляем в предложенные уравнения значения координат х, у заданных точек:

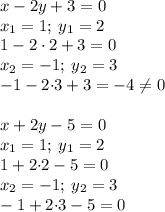
$x-2y+3=0 \\ x_{1} = 1;\:y_{1} = 2 \\ 1-2 \cdot2+3=0 \\ x_{2} = - 1;\:y_{2} = 3 \\{ -} 1-2{ \cdot}3+3= {- }4 \neq{0}\\ \\ x+2y-5=0 \\x_{1} = 1;\:y_{1} = 2 \\1 + 2{ \cdot}2 - 5 = 0 \\x_{2} = - 1;\:y_{2} = 3 \\ - 1 + 2{ \cdot}3 - 5 =0\\ \\$

Как видим, прямая, заданная уравнением

х + 2у - 5=0

включает в себя обе точки А и В.

Дальше можно не проверять: ведь через две точки можно провести только одну прямую.

Следовательно, будет такой

х + 2у - 5=0

2) "Честное" решение.

Прямая, проходящая через 2 заданные точки - единственна и задается уравнением следующего вида:

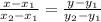
$\frac{x - x_{1}}{x_{2} - x_{1}} = \frac{y- y_{1}}{y_{2} - y_{1}} \\$

Подставим координаты заданных точек А и В:

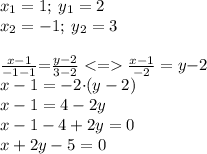
$x_{1} = 1;\:y_{1} = 2 \\x_{2} = - 1;\:y_{2} = 3 \\ \\ \small \frac{x {-} 1}{ {- }1 {- } {1}}{ =} \frac{y{- }2}{3{- }2} < = \frac{x {-} 1}{ - 2} = y{- }2 \\ x - 1 = - 2{ \cdot}(y - 2) \\ x - 1 = 4 - 2y \\ x - 1 - 4 + 2y = 0 \\ x + 2y - 5 = 0$

Это уравнение прямой

х + 2у - 5 = 0

и будет ответом в задаче.

х + 2у - 5=0

Nemsix

Алгебра

4,4(12 оценок)

ответ: На фото всё есть

Объяснение: Если нужно могу объяснить шаги

решите линейное уравнение 7,5−13+(4,88l)=12+7,5−5,12l.

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.