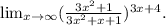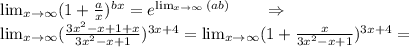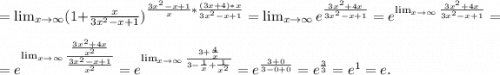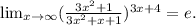,сегодня нужно сдать,а я никак не могу решить ( ) lim x → ∞ (3x2+1/3x2-x+1)^3x+4

198

500

Посмотреть ответы 3

Ответы на вопрос:

AMINA2007133456

Алгебра

4,5(63 оценок)

Объяснение:

тяжело записать, но попробую. пишите lim и степень за скобкой как указано. в скобке будет следующее: = (3x^2+1+x-x)/(3x^2-x+1)=(1+ x/(3x^2-x+1)=(1+1/x/(3x^2-x+1) это трехэтажная дробь, =(1+1/(3x^2-x+1)/x степень скобки будет (3x^2-x+1)/x, ставим еще скобку, за ней обратная степень х/(3x^2-x+1), эту домножаем на данную степень 3х+4. теперь убираем предел = е^lim(x*(3x+4))/(3x^2-x+1)=е^lim(3x^2+4x)/(3x^2-x+1)=e^1=e

vladrifeyt1

Алгебра

4,5(96 оценок)

Объяснение:

$\lim_{x \to \infty}(\frac{3x^2+1}{3x^2+x+1})^{3x+4}.$

Используем свойства второго замечательного предела:

$\lim_{x \to \infty} (1+\frac{a}{x})^{bx}=e^ \lim_{x \to \infty} {(ab)}}\ \ \ \ \ \ \Rightarrow\\ \lim_{x \to \infty} (\frac{3x^2-x+1+x}{3x^2-x+1})^{3x+4} = \lim_{x \to \infty} (1+\frac{x}{3x^2-x+1})^{3x+4} =\\$

$= \lim_{x \to \infty} (1+\frac{x}{3x^2-x+1} )^{\frac{3x^2-x+1}{x}*\frac{(3x+4)*x}{3x^2-x+1}}= \lim_{x \to \infty} e^\frac{3x^2+4x}{3x^2-x+1} =e^{ \lim_{x \to \infty} \frac{3x^2+4x}{3x^2-x+1}} = \\=e^{ \lim_{x \to \infty} \frac{\frac{3x^2+4x }{x^2} }{\frac{3x^2-x+1}{x^2} }} = e^ \lim_{x \to \infty} \frac{3+\frac{4}{x} }{3-\frac{1}{x} +\frac{1}{x^2} }}=e^\frac{3+0}{3-0+0} =e^\frac{3}{3} =e^1=e.$

ответ: $\lim_{x \to \infty}(\frac{3x^2+1}{3x^2+x+1})^{3x+4}=e.$

Alexander169

Алгебра

4,4(18 оценок)

-12

Объяснение:

Другие значения подставлять бессмысленно,выйдет гораздо меньше

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.