Регистрация Спросить otvet5GPT
kelyansky
07.06.2022 02:13
Алгебра
Есть ответ 👍

Докажите тождество хотя бы с 1 из 2

155
321
Посмотреть ответы 2

Ответы на вопрос:

diankakakutkin
diankakakutkin
4,4(66 оценок)

Объяснение:

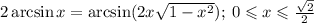
\small2 \arcsin{x} = \arcsin(2x \sqrt{1 - {x}^{2} } ); \: 0 \leqslant x \leqslant \frac{ \sqrt{2} }{2}

Рассмотрим по отдельности правую и левую часть тождества.

Т к имеются ограничения на значение х, для удобства можно произвести замену переменной:

x = \sin{y} ; \\

ограничив соответственно значение у пределами, такими что:

0 \leqslant y \leqslant \tfrac{\pi}{4} < = \sin{0} \leqslant \sin{y}{ =} x \leqslant \sin \tfrac{\pi}{4} \\ 0 \leqslant x \leqslant \tfrac{ \sqrt{2} }{2} \:

После замены получаем следующее выражение. В левой части будет:

\small2 \arcsin{( \sin{y}) } = 2y; \: 0 \leqslant y \leqslant \tfrac{\pi}{4} ;

В правой части:

\arcsin(2x \sqrt{1 - {x}^{2} } ) = \\ = \arcsin \big(2 \sin{y} \sqrt{1 - \sin {}^{2}y } \big)

так как для

\forall{y} \in [0;\tfrac{\pi}{4}]\: \sin{y} \geqslant 0; \: \cos{y} \geqslant 0

то можем преобразоватт выражение в правой части следующим образом:

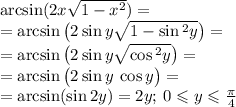
\arcsin(2x \sqrt{1 - {x}^{2} } ) = \\ = \arcsin \big(2 \sin{y} \sqrt{1 - \sin {}^{2}y } \big) = \\= \arcsin \big(2 \sin{y} \sqrt{ \cos {}^{2}y } \big) = \\ = \arcsin \big(2 \sin{y} \: \cos {y} \big) = \\ = \arcsin( \sin{2y}) =2y; \: 0 \leqslant y \leqslant \frac{ \pi}{4}

В результате, как мы видим, и в правой и в левой части мы получили одно и то же выражение. Следовательно, тождество верно

dashabalybina11
dashabalybina11
4,7(50 оценок)
№№2 вектор р=(2; -5)

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS