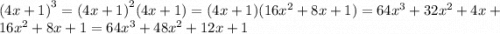Регистрация Спросить otvet5GPT
cherkashina711
02.01.2021 11:16
Алгебра
Есть ответ 👍

Возведите в куб сумму 4x+1.​

132
392
Посмотреть ответы 3

Ответы на вопрос:

nikysha04
nikysha04
4,4(64 оценок)

1)Д

2)В

Объяснение:

{(4x + 1)}^{3} = {(4x + 1)}^{2} (4 x+ 1) = (4x + 1)(16 {x}^{2} + 8x + 1) = 64 {x}^{3} + 32 {x}^{2} + 4x + 16 {x}^{2} + 8x + 1 = 64 {x}^{3} + 48 {x}^{2} + 12x + 1

16 {}^{2} -32×12+12 {}^{2} = {16}^{2} - 2 \times 16 \times 12 + {12}^{2} = {(16 - 12)}^{2} = {4}^{2} = 16

arisha20003000
arisha20003000
4,4(14 оценок)

Объяснение:

(а+b) ^3=a^3+3a^2b+3ab^2+b^3

(4х+1)^3=(4x)^3+3×(4x)^2×1+3×4x×1^2+1^3=

=64x^3+48x^2+12x+1

Oтвет : D)

А7

16^2-32×12+12^2=(16-12)^2=4^2=16

ответ : В)

dedpul23
dedpul23
4,7(40 оценок)

1. (x-2)√(x+5)/(x-3)√(x+3)≥0

вспоминаем про квадратный корень, что он всегда больше равен 0 и что подкоренное выражение всегда также больше равно 0. и знаменатель не равен 0

итак (x+5)≥0   x≥-5

x+3> 0 x> 0

x-3≠0 x≠3

одз x∈(-3 3) u (3 + ∞)

одзз нашли значит корни можно отбросить так как они всегда больше равны 0

(x-2)/(x-3)≥0

используем метод интервалов находим интервалы и пересекаем с одз

++++++++++[2] (3) +++++++++ (рисунок)

x∈(-∞ 2] u (3 +∞)∞ и пересекаем с одз x∈(-3 3) u (3 + ∞)

ответ x∈(-3 2] u (3 + ∞)

2. (x+1)(x-2)√(3-x)(x+2) > 0

одз подкоренное выражение больше (равно на этот раз не надо , так как строгое неравенство) 0

(3-x)(x+2)> 0 опять метод интервалов

(-2) +++++++++++ (3)

x∈(-2 3)

опять одз нашли отбрасываем корень так как он больше 0 и методом интервалов решаем неравенство   (x+1)(x-2) > 0 и пересекаем с одз

+++++++++ (-1) (2) +++++++++

x∈(-∞ -1) u (2 +∞)   и пересекаем с   x∈(-2 3)

ответ х∈(-2 -1) u (2 3)

==============================================

нравится решение ставь лайк и лучший

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS