В ответе укажите число решений, принадлежащих интервалу [0;2П] + дам лучший ответ
Ответы на вопрос:
4
Объяснение:
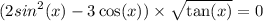
а)ОДЗ:
{ tan(x) ≥0 (Т.к. подкоренное выражение всегда неотрицательно)
{ cos(x) ≠0 (Т.к. тангенс это синус, делённый на косинус,а на ноль делить нельзя)
Произведение равно нулю,когда хотя бы один из множителей равен нулю
1) 2sin²(x)-3cos(x) = 0
Из основного тригонометрического тождества sin²(x)+cos²(x) = 1 выразим синус
sin²(x) = 1-cos²(x)
2(1-cos²(x))-3cos(x) = 0
2-2cos²(x)-3cos(x) = 0|:(-1)
2cos²(x)+3cos(x)-2 = 0
Пусть cos(x) = t, -1 ≤ t ≤ 1, тогда
2t²+3t-2 = 0
D = 3²-4*2*(-2) = 9+16 = 25 = 5²
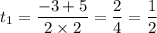
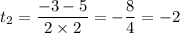
Второй корень меньше -1,поэтому мы его рассматривать не будем
Вернёмся к замене
Если t = 0,5, тогда
cos(x) = 0,5
Это равенство распадается на совокупность двух:
[ x = arccos(0,5) + 2пn, n∈Z
[ x = -arccos(0,5) + 2пn, n∈Z
[ x = п/3 + 2пn, n∈Z
[ x = -п/3 + 2пn, n∈Z
Второй корень не подходит по ОДЗ,так что единственное решение этого равенства x = п/3 + 2пn, n∈Z
2)
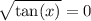


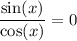
Дробь равна нулю,когда числитель равен нулю,а знаменатель не равен нулю
{ sin(x) = 0
{ cos(x) ≠ 0
{ х = пn, n∈Z
{ x ≠ п/2 + пn, n∈Z
Пересечений с ОДЗ нет,поэтому наше решение входит в ответ
б) Находим количество решений на отрезке [0;2П] ( см. вложение)
По рисунку мы видим,что у уравнения на данном отрезке 4 корня(0,п/3,п,2п)
![В ответе укажите число решений, принадлежащих интервалу [0;2П] + дам лучший ответ](/tpl/images/4515/4880/41216.jpg)
х=3. y=6
x=4. y=4 -исключаем так как не соответствуют
Объяснение:
обратите внимание на фото
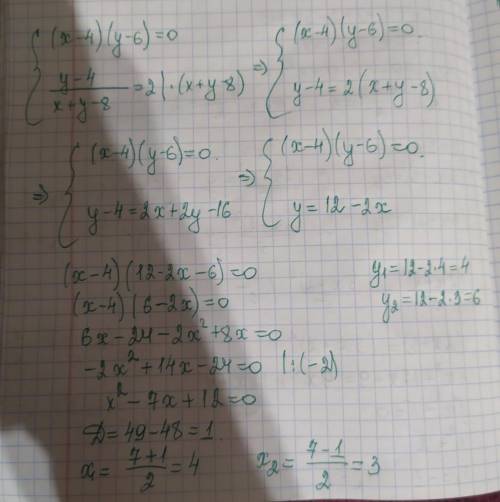
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
Решите систему уравнений методом замены переменных: {5 * x/y + (x/y)^2 =...
 SlavaRPSS24.03.2021 15:10
SlavaRPSS24.03.2021 15:10 -
Квадратичная функция задана формулой: у=-2x^2 + 6x + 3. найдите значение...
 алинка55401.07.2020 03:33
алинка55401.07.2020 03:33 -
Известно, что функция g в промежутке (0; +∞) принимает лишь отрицательные...
 ImperatorrPhysics10.10.2022 09:25
ImperatorrPhysics10.10.2022 09:25 -
Найдите значение выражение 2целых 5десятых ×2 в 4 степени минус 7 во 2 степени...
 хадЯ6602.05.2021 08:19
хадЯ6602.05.2021 08:19 -
Решить дано: треугольник авс , ас=вс, ав =12 , cos a = 2корня из 29 29 найти:...
 sergey07070720.06.2022 10:42
sergey07070720.06.2022 10:42 -
1)вычислите 2)вычислите 3)выполните действия tex] \frac{1}{5} \sqrt{225}-0.5...
 66456546501.07.2020 06:21
66456546501.07.2020 06:21 -
Знайдіть значення функції у = 2х - 1,5, якщо х...
 rudneva0422.01.2021 01:45
rudneva0422.01.2021 01:45 -
Сравни значения выражений A= 8⋅10−5 и B= 8⋅10−4. A B (Для ответа используй...
 memasov01.04.2022 08:06
memasov01.04.2022 08:06 -
буду очень благодарен. представить в виде произведения 1) √3 - tg x...
 123456uiop28.01.2020 22:46
123456uiop28.01.2020 22:46 -
Знайдіть суму шести перших членів геометричної прогресії (bn), якщо b5+b6=9,...
 Begzodik11.04.2022 03:09
Begzodik11.04.2022 03:09

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.
