Регистрация Спросить otvet5GPT
Confident23
20.04.2023 01:32
Алгебра
Есть ответ 👍

Нужна ❗❗❗❗❗❗ 1. корень из 48 + корень из 12, нужен максимально развёрнутый ответ, со стороны вроде бы легко, а уже 2 день разобраться не могу,
​

114
269
Посмотреть ответы 3

Ответы на вопрос:

nnursejt
nnursejt
4,6(58 оценок)

Объяснение:

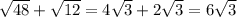
\sqrt{48} + \sqrt{12} = 4 \sqrt{3} + 2 \sqrt{3} = 6 \sqrt{3}

тут просто надо свести корни к одинаковому числу и после суммировать как числа с х, но вместо него √

Вольха97
Вольха97
4,4(25 оценок)

6√3

Объяснение:

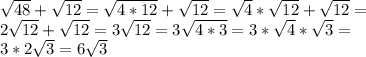
\sqrt{48}+\sqrt{12}=\sqrt{4*12}+\sqrt{12}=\sqrt{4}*\sqrt{12}+\sqrt{12}=\\2\sqrt{12}+\sqrt{12} =3\sqrt{12}=3\sqrt{4*3}=3*\sqrt{4}*\sqrt{3}=\\3*2\sqrt{3} =6\sqrt{3}

После второго и шестого знаков "равно" я воспользовался свойством арифметического квадратного корня: 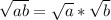\sqrt{ab}=\sqrt{a}*\sqrt{b}.

palechov01
palechov01
4,4(37 оценок)

ответ: 4

пошаговое решение:

1) выражение.

4(\tan^{2}a+\sin^{2}a+\cos^{2}a)\cos^{4}a=4(1+\tan^{2}a)\cos^{4}a=4\frac{\cos^{4}a}{\cos^{2}a}=4\cos^{2}a

2) так как не дано никаких ограничений по значению переменной a, то можно сказать, что наибольшего значения это выражение достигает при наибольшем косинусе, а наибольший возможный косинус равен 1. такое возможно, если a=2\pi n, n \in \mathbb{z}. таким образом, наибольшее значение данного выражения равно 4*1^2=4*1=4.

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS