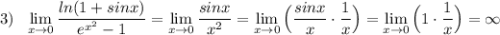Числовая последовательность задана формулой a^n=n^2+7.найдите сумму первых трех ее членов
211
321
Ответы на вопрос:
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
Решите уравнение x^2-4x=12...
 MatveiKnyaz200515.06.2023 23:00
MatveiKnyaz200515.06.2023 23:00 -
Компания Samokat каждый месяц производит три вида самокатов. Городских выпускают...
 22145119.03.2021 12:20
22145119.03.2021 12:20 -
, с заданием, скрин прикрепил...
 arsen7076ovwzre19.04.2021 20:28
arsen7076ovwzre19.04.2021 20:28 -
Решите, нужно а)решите уравнение sin п+х/2+cos(п+x)=1 б)найдите корни этого уравнения,принадлежащие...
 FireLily09.08.2021 01:03
FireLily09.08.2021 01:03 -
Решите графичеки эти уравнения, я не поняла как. там таблицу хотя бы, поняла только...
 kiranay200718.08.2020 15:49
kiranay200718.08.2020 15:49 -
Найдите наименьшее число n, чтобы произведение чисел от 2 до n делилось на 1992....
 toli4ka133715.02.2023 09:54
toli4ka133715.02.2023 09:54 -
Решить неравенство! log7 2x-6/2x-1 0...
 tomakor26.02.2020 21:48
tomakor26.02.2020 21:48 -
Если от задуманного трёхзначного числа отнять 9, то получившееся число разделится...
 kimttaehyung12.09.2021 22:33
kimttaehyung12.09.2021 22:33 -
Числа a и b натуральные. при делении на 17 число a даёт в остатке 9, а число b даёт...
 ilya20129618.08.2021 01:57
ilya20129618.08.2021 01:57 -
Найти число а если его целая часть составляет (-5), а дробная часть составляет 40%...
 Fhaj104.05.2023 11:03
Fhaj104.05.2023 11:03

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

![2)\ \ \lim_{n \to \infty}\dfrac{3n^{4/3}+\sqrt[3]{n^2-1}}{(n+\sqrt{n})^2}=\Big[\ \dfrac{:n^2}{:n^2}\ \Big]=\lim\limits _{n \to \infty}\dfrac{\frac{3}{n^{2/3}}+\sqrt[3]{\frac{1}{n^4}-\frac{1}{n^6}}}{1+\frac{2}{\sqrt{n}}+\frac{1}{n}}=\dfrac{0}{1}=0](/tpl/images/3914/1539/ffc02.png)