Регистрация Спросить otvet5GPT
AnnaMillerNikitina
22.11.2021 15:20
Алгебра
Есть ответ 👍

Log√5(x-4)≥0 можно решение этой неровности

124
130
Посмотреть ответы 2

Ответы на вопрос:

GasanDJ
GasanDJ
4,6(44 оценок)

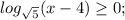
log_{\sqrt5}(x - 4) \geq 0;

Ноль можно записать как логарифм с основанием 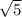\sqrt5.

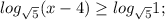
log_{\sqrt5}(x - 4) \geq log_{\sqrt5}1;

Т. к. основание логарифма 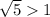\sqrt{5} 1, то логарифм можно опустить без изменения знака неравенства.

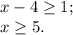
x - 4 \geq 1;\\x \geq 5.

ответ: 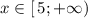x\in[\,5;+\infty).

MikhailMaksimovich
MikhailMaksimovich
4,7(33 оценок)
ыхкььцхф

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS