Найдите координаты точек пересечения окружности (х – 2)²+ (y – 4)²= 2 с прямой у =5
180
353
Ответы на вопрос:
-1 или -3
Объяснение:
(х – 2)²+ (5 – 4)²= 2
x²-4x+4+25-40+16=2
x²-4x+5=2
x²-4x+5-2=0
x²-4x+3=0
D=b²-4ac
D=16-4*1*3=16-12=4
![\sqrt[]{4}](/tpl/images/4092/8755/84d71.png) =2
=2
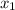 =
=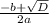
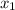 =
=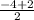 =
=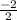 =-1
=-1
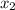 =
=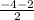 =
=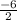 =-3
=-3
Подставим х=3 в уравнение окружности
(x-2)²+(y-4)²=2
получим
(3-2)²+(y-4)²=2
(y-4)²=3
y-4=√3 или у-4 =-√3
y=4+√3 или у=4-√3
ответ. (3; 4+√3) (3; 4-√3)
(x-2)²+(y-4)²=2
получим
(3-2)²+(y-4)²=2
(y-4)²=3
y-4=√3 или у-4 =-√3
y=4+√3 или у=4-√3
ответ. (3; 4+√3) (3; 4-√3)
Вписанный в правильную пирамиду шар касается основания пирамиды (в его центре и апофем пирамиды. то есть в сечении пирамиды по ее апофемам мы имеем равнобедренный треугольник со сторонами, равными апофкмам и основанием, равным стороне квадрата (основания). в этот треугольник вписана окружность (сечение шара). есть формула радиуса вписанной в треугольник окружности: r=s/p, где s- площадь треугольника, а р - его полупериметр. найдем высоту пирамиды по пифагору: √(10²-6²)=8 (10 - апофема, 6 - половина стороны квадрата). тогда площадь треугольника равна s=8*6=48. тогда радиус вписанной в треугольник окружности равен r=s/p= 48/16 = 3. это и есть радиус вписанного в пирамиду шара. второй вариант: по формуле радиуса вписанной в равнобедренный треугольник окружности: r=(b/2)*√[(2a-b)/(2a+b)]. в нашем случае: r=6*√(1/4) = 3. объем шара находим по формуле: v=(4/3)*π*r³ =36π. ответ v = 36π.
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Геометрия
-
Лабораторная работа № 1 Определение видов растений и животных (местного региона)...
 Sofia198601.04.2022 21:20
Sofia198601.04.2022 21:20 -
стадо равносторонней трапеции, диагонали которой перпендикулярны, а основания составляют...
 Verabogomaz11.12.2020 00:09
Verabogomaz11.12.2020 00:09 -
Үшбұрыштың биіктігі оның қабырғасына тең ...
 Lizka2285509.01.2023 07:37
Lizka2285509.01.2023 07:37 -
Найдите высоты треугольника со сторонами 17 65 и 80. (ответ запишите в виде смешанных...
 klimenkol2126.02.2021 04:08
klimenkol2126.02.2021 04:08 -
1.6. Торкөз қағазға, 1.6-суретте көрсетілгендей, АВ түзуі мен С нүктесін салыңдар....
 allanazarova1225.01.2021 02:08
allanazarova1225.01.2021 02:08 -
Средняя линия трапеции равна 10см.одна из диоганалей делит ее на два отрезка,разность...
 verailina199110.08.2021 18:15
verailina199110.08.2021 18:15 -
Найдите площадь прямоугольного треугольника, один из катетов которого равен 13,...
 Artem040510.01.2022 22:12
Artem040510.01.2022 22:12 -
2. Используя рисунок, заполните пропуски. 1) CBF и ...
 Brutal9408.12.2021 08:33
Brutal9408.12.2021 08:33 -
Сторона ромба 17 см, діагональ 16 см . Знайти другу діагональ...
 санеке03.11.2020 14:17
санеке03.11.2020 14:17 -
2 і 3 , будь ласка, дуже потрібно . ів . Повне пояснення , важлива контрольна,...
 mezhsaya28.08.2022 22:05
mezhsaya28.08.2022 22:05

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.
