Регистрация Спросить otvet5GPT
вованн2
16.04.2021 09:11
Математика
Есть ответ 👍

Тест 1
По рисунку докажите, что:
а) AC = BD, AD = ВС,
б) CAD =DBC.​

250
491
Посмотреть ответы 1

Ответы на вопрос:

danyabro1
danyabro1
4,4(63 оценок)

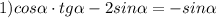
1) cos \alpha \cdot tg\alpha -2 sin\alpha=-sin\alpha

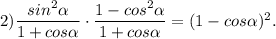
2) \dfrac{sin^{2} \alpha }{1+cos\alpha } \cdot \dfrac{1-cos^{2}\alpha }{1+cos\alpha }=(1-cos\alpha )^{2} .

Пошаговое объяснение:

1) Упростим выражение

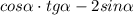
cos \alpha \cdot tg\alpha -2 sin\alpha

Воспользуемся формулой

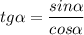
tg\alpha =\dfrac{sin\alpha }{cos\alpha }

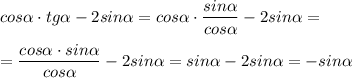
cos \alpha \cdot tg\alpha -2 sin\alpha=cos \alpha \cdot \dfrac{sin\alpha }{cos\alpha } -2 sin\alpha == \dfrac{cos\alpha \cdot sin\alpha }{cos\alpha } -2sin\alpha =sin\alpha -2sin\alpha =-sin\alpha

2) Упростим выражение

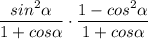
\dfrac{sin^{2} \alpha }{1+cos\alpha } \cdot \dfrac{1-cos^{2}\alpha }{1+cos\alpha }

Представим по основному тригонометрическому тождеству

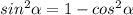
sin^{2} \alpha =1-cos^{2} \alpha

и разложим на множители, применяя формулу сокращенного умножения

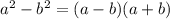
a^{2} -b^{2} =(a-b)(a+b)

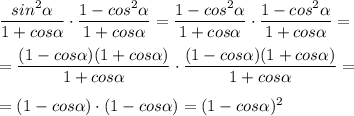
\dfrac{sin^{2} \alpha }{1+cos\alpha } \cdot \dfrac{1-cos^{2}\alpha }{1+cos\alpha }=\dfrac{1-cos^{2}\alpha }{1+cos\alpha } \cdot \dfrac{1-cos^{2}\alpha }{1+cos\alpha }==\dfrac{(1-cos\alpha)(1+cos\alpha ) }{1+cos\alpha } \cdot \dfrac{(1-cos\alpha)(1+cos\alpha ) }{1+cos\alpha }==(1-cos\alpha )\cdot(1-cos\alpha )=(1-cos\alpha )^{2}

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS