Математика: 123456789*123456789/123456789-123456789+123456789=

Melba

02.12.2020 09:54

Математика

Есть ответ 👍

123456789*123456789/123456789-123456789+123456789=

249

455

Посмотреть ответы 3

Ответы на вопрос:

Fanapav

Математика

4,8(13 оценок)

123456789

Пошаговое объяснение:

Batman781

Математика

4,7(99 оценок)

123456789*123456789/123456789-123456789+123456789=123456789

abcdefgh

Математика

4,7(38 оценок)

Дано:

△ABC - равнобедренный;

P△ABC = 36, AB = 16.

Найти:

S△ABC = ? (ед. кв).

Решение:

Т.к. △ABC - равнобедренный ⇒ AC = CB, по свойству равнобедренного тр-ка.

Предположим, что основание составляет 16. Тогда:

AC = CB = (36 - 16) : 2 = 20 : 2 = 10.

Проверим, верно ли это по теореме о неравенстве тр-ка.

"Каждая сторона треугольника меньше суммы двух других сторон".

⇒ 16 + 10 > 10, 10 + 10 > 16, 10 + 16 > 16 (всё совпадает, поэтому боковую сторону и основание мы нашли верно).

Формула площади треугольника выглядит следующим образом:

S△ = 1/2 ⋅ a ⋅ h, где a - основание (AB), h - высота.

Проведём из точки B к основанию равнобедренного тр-ка высоту CH. При этом у нас образовалось два равных прямоугольных треугольника ACH и BCH (их равенство можно доказать по всем признакам равенства прямоугольных тр-ков, исходя из того, что △ABC - равнобедренный).

"В равнобедренном треугольнике высота, проведённая к основанию, является медианой и биссектрисой".

⇒ CH является медианой и делит основание AB так, что AH = HB = 16 : 2 = 8.

Найдём высоту равнобедренного тр-ка ABC по теореме Пифагора (a = √(c² - b²), где a и b - катеты, c - гипотенуза).

CH = √(AC² - AH²) = √(10² - 8²) = √(100 - 64) = √36 = 6.

CH = √(CB² - HB²) = √(10² - 8²) = √(100 - 64) = √36 = 6.

Найдём площадь равнобедренного тр-ка ABC по указанной выше формуле:

S△ABC = 1/2 ⋅ 16 ⋅ 6 = 16/2 ⋅ 6 = 8 ⋅ 6 = 48 (ед. кв).

ответ: 48 (ед. кв).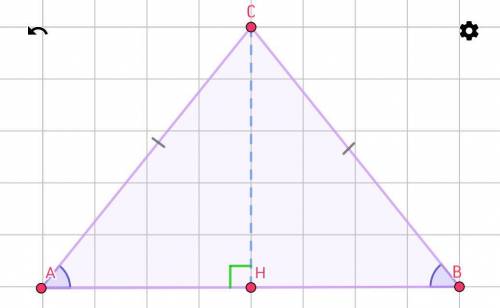
ABC-равнобедренний треугольникP=36AB=16Ниайдите Площадь

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.