1. Треугольник АВС и квадрат АЕFC не лежат в одной плоскости. Точки К и М - середины отрезков АВ и ВС соответственно. Докажите, что КМ││EF. Найдите КМ, если АЕ = 15 см. 2. Точка А лежит в плоскости , параллельной прямой а. Через точку А проведена прямая b, параллельная прямой а. Докажите, что прямая b лежит в плоскости .
3. Прямые а и b параллельны. Через точку В, лежащую на прямой b, проведена плоскость , параллельная прямой а. Докажите, что плоскость проходит через прямую b.
4. В треугольнике АВС на стороне АВ выбрана точка D, такая, что BD: ВА = 1:4. Плоскость, параллельная прямой АС и проходящая через точку D, пересекает отрезок ВС в точке D1. Докажите, что треугольник DВ D1 подобен треугольнику АВС. Найдите АС, если DD1= 9,5см.
5. Плоскости и пересекаются по прямой с. Плоскость , параллельная прямой с, пересекает плоскости и по прямым а и в соответственно. Докажите , что а││ и b││а.

249

296

Посмотреть ответы 1

Ответы на вопрос:

vitashe135

Геометрия

4,8(63 оценок)

∠B = 45°; ∠C = 15°; AB ≈ 0.732 см;

Объяснение:

Дано:

ΔАВС

ВС = √6 см

АС = 2 cм

∠А = 120°

Найти:

∠В; ∠С; АВ;

По теореме синусов

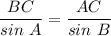
$\dfrac{BC}{sin~A} =\dfrac{AC}{sin~B}$

Откуда

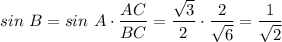
$sin~B = sin~A\cdot \dfrac{AC}{BC} = \dfrac{\sqrt{3} }{2} \cdot \dfrac{2}{\sqrt{6} } = \dfrac{1}{\sqrt{2} }$

∠B = 45°

По свойству углов треугольника

∠С = 180° - (∠А + ∠В) = 180° - (120° + 45°) = 15°;

По теореме синусов

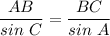
$\dfrac{AB}{sin~C} =\dfrac{BC}{sin~A}$

Откуда

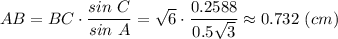
$AB = BC\cdot \dfrac{sin~C}{sin~A} = \sqrt{6} \cdot \dfrac{0.2588}{0.5\sqrt{3} } \approx 0.732 ~(cm)$

Задай свой вопрос

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.