Ответы на вопрос:
квадратное уравнение может иметь один или два корня. значит, из трёх чисел можно составить шесть (см. об этом ниже) уравнений: с корнями (2), (5), (9), (2; 5), (2; 9), (5; 9).
составим уравнения с одним корнем — это будут полные квадраты:
далее составим уравнения с двумя корнями. используем теорему виета: коэффициенты уравнения вычисляются по формулам
.
первое уравнение (2; 5):
второе уравнение (2; 9):
третье уравнение (5; 9):
ответ: шёсть уравнений:
а теперь рассмотрим уравнения — в которых коэффициент при не равен единице (и нулю, конечно, поскольку тогда уравнение перестаёт быть поскольку любое квадратное уравнение
можно разложить на множители:
и в этом разложении при любом оно будет иметь те же корни, то таких уравнений можно составить бесконечное количество. например, если взять уравнение
и умножить его на любое число (кроме нуля):
— то его корни останутся прежними.
окончательный ответ: с данными корнями можно создать бесконечное количество уравнений.
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
Решите уравнение: (х-5)(х+5)=(х-3)в крадрате+2 сократите дробь:...
 Mishanaxsar28.07.2021 22:32
Mishanaxsar28.07.2021 22:32 -
V- это корень v 11-2v5 11-22 все корень как это...
 яна176504.10.2022 16:11
яна176504.10.2022 16:11 -
Выразите переменную p из переменной c = dp - 5...
 sofa28726.05.2023 02:41
sofa28726.05.2023 02:41 -
Найдите наибольшее значение функции f (x) = 18(0,5x – 2)^2 – (0,5x...
 lassdeavs31.03.2022 19:03
lassdeavs31.03.2022 19:03 -
Выражения 1+sin (п/2-a)cos(п-a)-sin в квадрате а . *...
 Ульяна273207.07.2020 07:10
Ульяна273207.07.2020 07:10 -
Помгите преобразовать в многочлен ( 9х-у) в квадрате...
 vanyushagrechk16.01.2023 21:03
vanyushagrechk16.01.2023 21:03 -
При каких значения параметра p неравенство (p-2)x^2+(p-3)x+p 0...
 Алёнушка4326.04.2023 17:39
Алёнушка4326.04.2023 17:39 -
Вклассе мальчиков в два раза больше, чем девочек. если из этого...
 lsofa120409.01.2020 11:46
lsofa120409.01.2020 11:46 -
Выражение (sin a + cos a ) в квадрате - sin 2 a +3. *...
 Bazzaevat12.02.2021 09:01
Bazzaevat12.02.2021 09:01 -
Sin(9x)=2sin(3x) через формулы 3-го аргумента...
 Kvodan12325.05.2020 23:02
Kvodan12325.05.2020 23:02

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

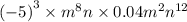 бірмүшесін стандарт түрге келтіріңіз. [3]
бірмүшесін стандарт түрге келтіріңіз. [3]