21.08.2022 02:58

Есть ответ 👍

Oбчисліть висоту трикутника проведену до вершини кута b якщо кут abc = 120 градусів ab= 6 см площа трикутника =6√3

115

272

Посмотреть ответы 1

Ответы на вопрос:

МалееваМария07

Геометрия

4,6(21 оценок)

Площадь сечения равна 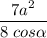$\displaystyle \frac{7a^2}{8\;cos\alpha }$ .

Объяснение:

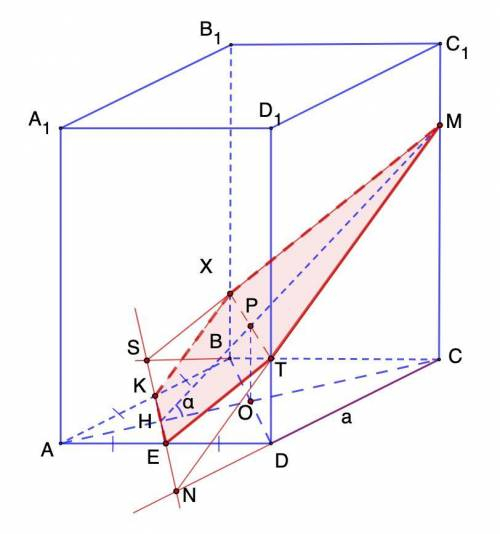
В правильной четырехугольной призме через середины двух смежных сторон основания проходит плоскость, которая образует с основанием призмы угол α и пересекает три боковых ребра. Найти площадь сечения, если сторона основания призмы А.

Построим сечение.

В основании правильной призмы лежит квадрат.

Отметим середины сторон АВ и AD и поставим точки К и Е соответственно. Соединим их.

Проведем диагонали АС и BD.

КЕ ∩ АС = Н.

Построим угол с вершиной в точке Н, равный α.

НР ∩ СС₁ = М.

Строим сечение, проходящее через три точки.

Продлим КЕ до пересечения с СВ и CD и поставим точки S и N соответственно.

S ∈ BB₁C₁C; M ∈ BB₁C₁C ⇒ S и M соединяем;

SM ∩ BB₁ = X;

N ∈ DD₁C₁C; M ∈ DD₁C₁C ⇒ N и M соединяем;

NM ∩ DD₁ = T;

X ∈ AA₁B₁B; K ∈ AA₁B₁B ⇒ X и K соединяем;

T ∈ AA₁D₁D; E ∈ AA₁D₁D ⇒ T и E соединяем;

EKXMT - искомое сечение.

Сечение представляет пятиугольник, состоящий из трапеции ЕКХТ и треугольника ХМТ.

⇒ S( EKXMT) = S(ЕКХТ) + S(ХМТ)

1. Рассмотрим ΔABD - прямоугольный.

AD = AB = a (условие)

По теореме Пифагора найдем BD:

BD² = AD² + AB² = 2a²

BD = a√2

ЕК - средняя линия ΔАВD.

Средняя линия равна половине длины стороны, которую она не пересекает.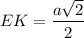

⇒ $\displaystyle EK = \frac{a\sqrt{2} }{2}$ - меньшее основание ЕКХТ.

2. Рассмотрим ΔНРО - прямоугольный.

∠РНО = α (условие).

Диагонали квадрата равны и точкой пересечения делятся пополам.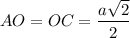

⇒ $\displaystyle AO = OC = \frac{a\sqrt{2} }{2}$

Средняя линия треугольника делит пополам любой отрезок, соединяющий вершину треугольника с какой-либо точкой основания.

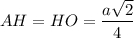
⇒ $\displaystyle AH=HO=\frac{a\sqrt{2} }{4}$

Косинус угла - отношение прилежащего катета к гипотенузе.

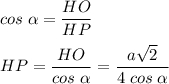$\displaystyle cos\;\alpha =\frac{HO}{HP} HP = \frac{HO}{cos\;\alpha }=\frac{a\sqrt{2} }{4\;cos\;\alpha }$ - высота ЕКХТ.

ХТ = BD = a√2 - большее основание ЕКХТ.

3. Найдем площадь трапеции.

Площадь трапеции равна произведению полусуммы оснований на высоту.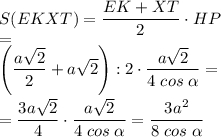

$\displaystyle S(EKXT)=\frac{EK+XT}{2}\cdot{HP}\\=\\\left(\frac{a\sqrt{2} }{2} +a\sqrt{2}\right):2\cdot{\frac{a\sqrt{2} }{4\;cos\;\alpha } } ==\frac{3a\sqrt{2} }{4}\cdot{\frac{a\sqrt{2} }{4\;cos\;\alpha } } =\frac{3a^2}{8\;cos\;\alpha }$

4. Рассмотрим ΔНМС - прямоугольный.

НС = НО + ОС

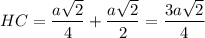
$\displaystyle HC= \frac{a\sqrt{2} }{4}+\frac{a\sqrt{2} }{2}=\frac{3a\sqrt{2} }{4}$

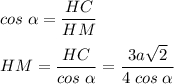
$\displaystyle cos\;\alpha =\frac{HC}{HM} HM=\frac{HC}{cos\;\alpha } =\frac{3a\sqrt{2} }{4\;cos\;\alpha }$

Тогда РМ = НМ - НР

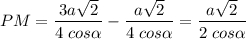
$\displaystyle PM =\frac{3a\sqrt{2} }{4\;cos\alpha } -\frac{a\sqrt{2} }{4\;cos\alpha } =\frac{a\sqrt{2} }{2\;cos\alpha }$

5. Найдем площадь ΔХМТ.

Площадь треугольника равна половине произведения стороны на высоту, проведенную к этой стороне.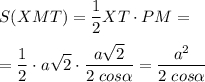

$\displaystyle S(XMT)=\frac{1}{2}XT\cdot{PM} ==\frac{1}{2}\cdot{a} \sqrt{2} \cdot{\frac{a\sqrt{2} }{2\;cos\alpha } }=\frac{a^2}{2\;cos\alpha }$

6. Теперь можем найти площадь сечения:

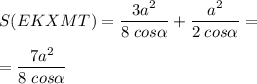
$\displaystyle S(EKXMT) = \frac{3a^2}{8\;cos\alpha }+\frac{a^2}{2\; cos\alpha }=\\ \\ =\frac{7a^2}{8\;cos\alpha }$

Площадь сечения равна 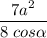$\displaystyle \frac{7a^2}{8\;cos\alpha }$ .

#SPJ1

У правильній чотирикутній призмі через середини двох суміжних сторін основи проходить площина, яка у

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.