Математика: Найдите Корни симметрического многочлена x⁴+2x³-x²+2x+1

Rezars19

05.08.2022 03:39

Есть ответ 👍

Найдите Корни симметрического многочлена
x⁴+2x³-x²+2x+1

270

422

Посмотреть ответы 2

brenczan

Математика

4,6(86 оценок)

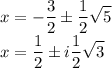
$\displaystyle x=-\frac32\pm\frac12\sqrt5\\x=\frac12\pm i\frac12\sqrt3$

Пошаговое объяснение:

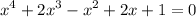
$\displaystyle x^4+2x^3-x^2+2x+1=0$

х = 0 - не является корнем данного многочлена, это значит, что мы можем поделить обе части на х².

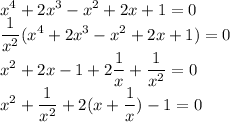
$\displaystyle x^4+2x^3-x^2+2x+1=0\\\frac1{x^2}(x^4+2x^3-x^2+2x+1)=0\\x^2+2x-1+2\frac1x+\frac1{x^2}=0\\x^2+\frac1{x^2}+2(x+\frac1x)-1=0$

Сделаем замену

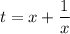
$\displaystyle t=x+\frac1x$

Тогда

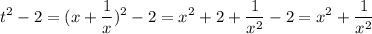
$\displaystyle t^2-2=(x+\frac{1}{x})^{2}-2=x^2+2+\frac{1}{x^2}-2=x^2+\frac{1}{x^2}$

Перепишем уравнение

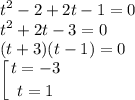
$\displaystyle t^2-2+2t-1=0\\t^2+2t-3=0\\(t+3)(t-1)=0\\\left [ {{t=-3} \atop {t=1}} \right. \\$

Мы нашли значение t. Осталось сделать обратную замену и решить это уравнение.

Буду решать каждое уравнение по отдельности.

1) t = -3

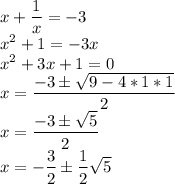
$\displaystyle x+\frac1x=-3\\x^2+1=-3x\\x^2+3x+1=0\\x=\frac{-3\pm\sqrt{9-4*1*1}}{2}\\x=\frac{-3\pm\sqrt5}{2}\\x=-\frac32\pm\frac12\sqrt5$

2) t = 1

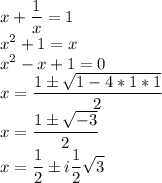
$\displaystyle x+\frac1x=1\\x^2+1=x\\x^2-x+1=0\\x=\frac{1\pm\sqrt{1-4*1*1}}{2}\\x=\frac{1\pm\sqrt{-3}}{2}\\x=\frac12\pm i\frac12\sqrt3$

Мы нашли все корни!

lilyabelousova

Математика

4,5(88 оценок)

Через 44

Задай свой вопрос

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.