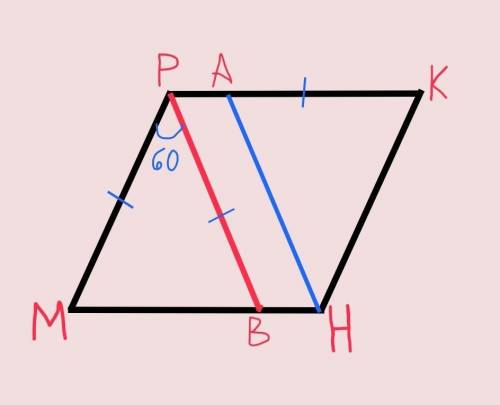
на сторонах PK и MH параллелограмма MPKH взяты точки A и B соответственно , MP=PB=AK , угол MPB =60°. найдите углы параллелограмма и сравните отрезки BM и побыстрее

231

287

Посмотреть ответы 2

Ответы на вопрос:

stefaniya2008

Геометрия

4,4(33 оценок)

Объяснение:

Так как МР=РВ по условию, то ∆МРВ – равнобедренный. Углы при основании равнобедренного треугольника равны, а сумма всех углов равна 180°.

Тогда угол PMB=угол РВМ=(180°–МРВ)÷2=(180°–60°)÷2=60°.

Получим что все углы ∆МРВ равны 60°, тогда ∆МРВ – равносторонний.

Тогда МВ=МР.

Углы при одной стороне параллелограмма в сумме равны 180°.

Значит угол МРК=180°–угол РМВ=180°–60°=120°

Противоположные углы параллелограмма равны.

Следовательно угол РКН=угол РМН=60°; угол МНК=угол МРК=120°.

МР=АК по условию

МР=КН так как противоположные стороны параллелограмма равны.

Углы при основании равнобедренного треугольника равны, а сумма всех углов равна 180°.

Следовательно: угол КАН=угол КНА=(180°–угол АКН)÷2=(180°–60°)÷2=60°.

Получим что все углы ∆АКН равны 60°, тогда ∆АКН – равносторонний. Исходя из этого АН=АК

МВ=МР=АК=АН => МВ=АН.

ответ: 1) 60°; 120; 2) равны.

на сторонах PK и MH параллелограмма MPKH взяты точки A и B соответственно , MP=PB=AK , угол MPB =60°

Няша200411

Геометрия

4,5(85 оценок)

Так как треугольник abc тупой то уголb> 90 отсюда следует что сумма углов а и с < 90угол в> угол а + угол с против ad лежит угол bпротив ав лежит угол с так как угол а заведомо не 0. то угол в> > угол c против большего угла лежит большая сторона => что и требовалось доказать

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.