Регистрация Спросить otvet5GPT
rika060501
15.05.2022 23:20
Алгебра
Есть ответ 👍

ЗАРАНЕЕ биквадратные уравнения*

288
404
Посмотреть ответы 3

Ответы на вопрос:

kotovak27
kotovak27
4,5(90 оценок)

1.

х⁴+3х²-70=0

сделаем замену:

х²=t

ОДЗ:

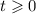
t \geqslant 0

получим уравнение :

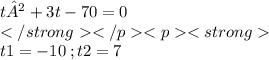
t²+3t-70=0 \\ \\ t1=-10 \: ; t2=7

первый корень меньше нуля поэтому он не подходить ОДЗ

возвращаемся к замене:

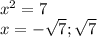
{x}^{2} = 7 \\x = - \sqrt{7};\sqrt{7}

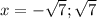
x = - \sqrt{7} ; \sqrt{7}

2.

9х⁴-10х²+1=0

делаем замену:

х²=t

ОДЗ:

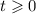
t \geqslant 0

получаем уравнение:

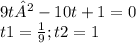
9t²-10t+1=0 \\ t1 = \frac{1}{9};t2 = 1

возвращаемся к замене:

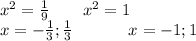
{x}^{2} = \frac{1}{9} \: \: \: \: \: \: \: \: \: {x}^{2} = 1 \\ x = - \frac{1}{3} ; \frac{1}{3} \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: x = - 1;1

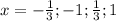
x= - \frac{ 1}{3} ; - 1; \frac{1}{3};1

3.

2х⁴-5х²+2=0

замена:

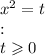
{x}^{2} = t \\ОДЗ: \\ t \geqslant 0

получаем уравнение:

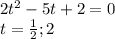
2t ^{2} - 5 t + 2 = 0 \\ t = \frac{1}{2} ;2

возвращаемся к замене:

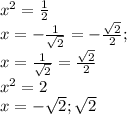
{x}^{2} = \frac{1}{2} \\ x = - \frac{1}{ \sqrt{ 2}} = - \frac{ \sqrt{2} }{2} ; \\ x = \frac{1}{ \sqrt{2} } = \frac{ \sqrt{2} }{2} \: \: \: \: \: \: \\ {x}^{2} = 2 \\ x = - \sqrt{2} ; \sqrt{2}

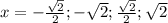
x = - \frac{ \sqrt{2} }{2}; - \sqrt{2}; \frac{ \sqrt{2} }{2}; \sqrt{2}

KsushaGromova
KsushaGromova
4,5(20 оценок)

x^4+3x^2-70=0

Обозначим x^2 = t

Решаем уравнение t^2 + 3t - 70 = 0

D = 289 . t = (-3 + 17 )/2 = 7

х^2 = 7 x = +- корень кв, из 7

9x^4-10x^2+1=0

Пусть х^2=t, тогда:

9t^2-10t+1=0

D=b^2-2ac

D=100-4*9*1=64

t1=1

t2=1/9

1)x^2=1; x=1

2)x^2=1/9; x=1/3

ответ: 1;1/3.

2x^4-52^2+2=0-а это не получается. Надеюсь чем могла

Объяснение:

qwweee
qwweee
4,8(22 оценок)
A- ширина, b - длина, h - высота

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS