Superstylegir

17.05.2022 18:33

Есть ответ 👍

Решить 11:3x-1-31
25 и указать
4:9x-11:3x-1-5
наименьшее целое
Неотрицательное число, входящее в решение.

185

463

Посмотреть ответы 2

Ответы на вопрос:

Coffee1998

Алгебра

4,7(65 оценок)

Замена переменной:

$3^{x}=t$

t 0

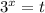
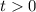
тогда

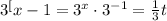
$3^[x-1}=3^{x}\cdot 3^{-1}=\frac{1}{3} t$

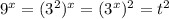
$9^{x}=(3^{2})^{x}=(3^{x})^{2}=t^2$

Неравенство принимает вид:

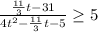
$\frac{\frac{11}{3}t-31}{4t^2-\frac{11}{3}t-5}\geq 5$

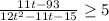
$\frac{11t-93}{12t^2-11t-15}\geq 5$

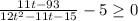
$\frac{11t-93}{12t^2-11t-15}-5\geq 0$

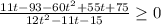
$\frac{11t-93-60t^2+55t+75}{12t^2-11t-15}\geq 0$

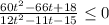
$\frac{60t^2-66t+18}{12t^2-11t-15}\leq 0$

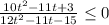$\frac{10t^2-11t+3}{12t^2-11t-15}\leq 0$ D=121-120=1 и D=121+720=841=29²

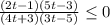
$\frac{(2t-1)(5t-3)}{(4t+3)(3t-5)}\leq 0$

Применяем метод интервалов:

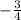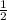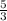___+__ ( $-\frac{3}{4}$ ) ___-__ [ $\frac{1}{2}$ ] __+__ [ $\frac{3}{5}$ ] __-__ ( $\frac{5}{3}$ ) __+__

C учетом t >0

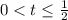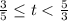
$0 < t \leq \frac{1}{2}$ или $\frac{3}{5 } \leq t < \frac{5}{3}$

Обратный переход:

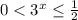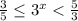
$0 < 3^{x} \leq \frac{1}{2}$ или $\frac{3}{5 } \leq 3^{x} < \frac{5}{3}$

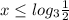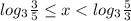
$x\leq log_{3}\frac{1}{2}$ или $log_{3}\frac{3}{5 } \leq x < log_{3}\frac{5}{3}$

$x\leq -1$ или x=0

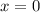
О т в е т. x=0 -наименьшее целое неотрицательное

Aynur123455

Алгебра

4,8(51 оценок)

(81-(41+10): 81=0,39

Задай свой вопрос

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.