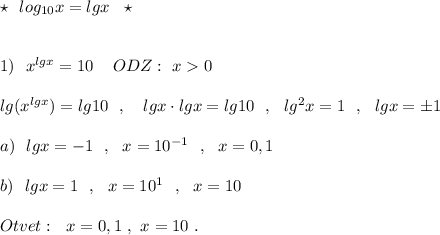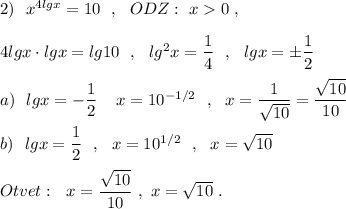полное решение со всеми пояснениями действий решений показательного уравнения: 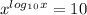
126
386
Ответы на вопрос:
ответ: .
.
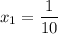 ;
; 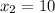
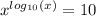
ОДЗ: 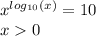
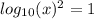
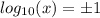
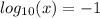
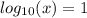
 .
.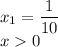
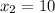
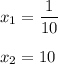
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
Разложите на множители x^3+3x^2-4x-12...
 sunlight212.04.2021 00:52
sunlight212.04.2021 00:52 -
1.найдите координаты точки пересечения графиков функции y=7x+1 и y=6x+2...
 Andrebro923.01.2021 19:41
Andrebro923.01.2021 19:41 -
Знайти два числа сума яких дорівнюэ 146,а різниця 28....
 Kurakluk09.03.2022 09:17
Kurakluk09.03.2022 09:17 -
Запиши в виде неравенства : а)семь больше одного б)минус три меньше...
 SofiLand85417.11.2022 22:13
SofiLand85417.11.2022 22:13 -
Разложите на множители: а) a(a+3)-2(a+3) б) ax-ay+5y-5y , прощу заранее...
 полина205407.02.2023 09:56
полина205407.02.2023 09:56 -
При каком значении а выражение 3+ а/х+5 тождественно равно дроби 3х/х+5?...
 uvar1313107.01.2021 14:26
uvar1313107.01.2021 14:26 -
Решите уравнение (5х+1)в квадрате=400...
 55555Даша1111111111123.06.2022 22:43
55555Даша1111111111123.06.2022 22:43 -
Вквадратном уравнении ах^2+bx+c=0 каждый из коэффициентов пределяется...
 dndwp0a74804.02.2020 14:08
dndwp0a74804.02.2020 14:08 -
35у+8+30у=47-20у-39 решите уравнение...
 0AlikaLi004.08.2020 23:35
0AlikaLi004.08.2020 23:35 -
Дана фигура P a) Отразите фигуру Р относительно оси ОУ и обозначьте...
 віка81227.05.2021 14:18
віка81227.05.2021 14:18

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.