Регистрация Спросить otvet5GPT
maxim1213
19.04.2022 16:20
Алгебра
Есть ответ 👍

Даны положительные действительные числа x, y, z, для которых x+y+z= 6. Докажите, что 108 > ху^2 z^3​

121
194
Посмотреть ответы 2

Ответы на вопрос:

дашенька158
дашенька158
4,5(69 оценок)

Существует всего 10 комбинаций, при которых х+у+z=6;

1) 1+2+3;

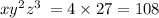
x {y}^{2} {z}^{3} \: = 4 \times 27 = 108

108 = 108;

2) 1+3+2;

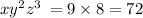
x {y}^{2} {z}^{3} \: = 9 \times 8 = 72

108 > 72;

3) 2+3+1;

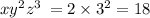
x {y}^{2} {z}^{3} \: = 2 \times {3}^{2} = 18

108 > 18;

4) 2+1+3;

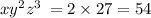
x {y}^{2} {z}^{3} \: = 2 \times 27 = 54

108 > 54;

5) 3+2+1;

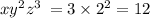
x {y}^{2} {z}^{3} \: = 3\times {2}^{2} = 12

108 > 12;

6) 3+1+2;

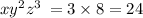
x {y}^{2} {z}^{3} \: = 3 \times 8 = 24

108 > 24;

7) 2+2+2;

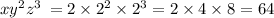
x {y}^{2} {z}^{3} \: = 2 \times {2}^{2} \times {2}^{3} = 2 \times 4 \times 8 = 64

108 > 64;

8) 1+1+4;

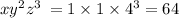
x {y}^{2} {z}^{3} \: = 1 \times 1 \times {4}^{3} = 64

108 > 64;

9) 1+4+1;

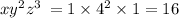
x {y}^{2} {z}^{3} \: = 1 \times {4}^{2} \times 1= 16

108 > 16;

10) 4+1+1;

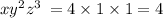
x {y}^{2} {z}^{3} \: = 4 \times 1 \times 1 = 4

108 > 4;

Что и требовалось доказать.

шедвер
шедвер
4,8(6 оценок)
Решение: для того, чтобы найти абсциссу точки пересечения графиков, приравняем правые части уравнений, эти функции: у = 8 - 4х, у = х + 14. решим уравнение: 8 - 4х = х + 14 -4х - х = -  8 + 14 -5х = 6 х = 6 : (-5) х = -1,2 ответ: - 1,2. замечание: использование при выполнении данных графического способа чревато неточностью и иногда даже невозможностью увидеть значение в изображённой  области координатной плоскости. (использование приложений не комментирую).

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS