Ответы на вопрос:
Если я правильно понял условие , то так. прямоугольный треугольник abc, где вс - гипотенуза. ва - больший катет, ас - меньший. пусть ас = x см, тогда ва = х+7. по теореме пифагора вс²=ва²+ас². подставляем значения. 13²=(х+7)²+х² 169=х²+14х+49+х² перенесём всё в левую часть и приравняем к 0. х²+х²+14х+49-169=0 2х²+14-120=0 теперь решаем через дискриминант а=2; в=14; с= -120 d=в² - 4ас d=1156 х₁ = -в+√d/2а= -14+√1156/4=5 х₂ можем не рассматривать, значение будет отрицательное. а сторона не может быть таковой. ⇒ х=5 теперь осталось подставить ас=5; ва = 5+7 = 12. ответ: катеты равны 5 и 12.
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
Найди значение выражения 2,09d−2,09b, если d=50,b=40....
 Роннилав23.07.2022 13:42
Роннилав23.07.2022 13:42 -
Рассматривая площадь Прямоугольника ABCD(рис 16) покажите что (a+b)...
 leila1234126.09.2020 20:27
leila1234126.09.2020 20:27 -
Решите уравнениe: x²-4x-140=0...
 лошадь2008.06.2020 00:15
лошадь2008.06.2020 00:15 -
Найти дискриминант квадратного уравнения...
 agarkovatanech11.07.2021 01:56
agarkovatanech11.07.2021 01:56 -
Решить систему методом Гаусса и по правилу Крамера...
 Glupiy77727.10.2021 21:54
Glupiy77727.10.2021 21:54 -
Найдите дискриминант данного уравнения. 5x²+x-6=0 Решите кратко,...
 nazarshariu7706.11.2021 11:53
nazarshariu7706.11.2021 11:53 -
Разложить на множители и вычислить, много . разложить на множители:...
 megachiglakov10.02.2020 02:21
megachiglakov10.02.2020 02:21 -
Две третьих умножить на одну четвертую 2/3*1/4...
 Лейла004415.08.2021 03:36
Лейла004415.08.2021 03:36 -
Освободитесь от иррациональности в знаменателе дроби 5/2√7...
 samat31414.11.2020 04:10
samat31414.11.2020 04:10 -
Какую сумму денег нужно положить в банк под 10% годовых чтоб через...
 olgauschap109.08.2021 19:00
olgauschap109.08.2021 19:00

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

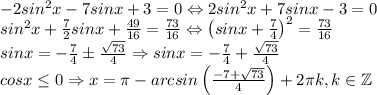
![\[x = \pi - \arcsin \frac{{7 - \sqrt {73} }}{{ - 4}} + 2\pi k,k \in {\bf{Z}}\]](/tpl/images/3784/5750/ff9f4.png)
![\[\begin{array}{l} - 2{\sin ^2}x - 7\sin x + 3 = 0\\\sin x = \frac{{7 \pm \sqrt {49 + 4 \cdot 2 \cdot 3} }}{{ - 2 \cdot 2}} = \frac{{7 \pm \sqrt {73} }}{{ - 4}}\end{array}\]](/tpl/images/3784/5750/a87e0.png)
![\[\sin x = \frac{{7 - \sqrt {73} }}{{ - 4}}\]](/tpl/images/3784/5750/a52ce.png)
![\[\begin{array}{l}\sin x = \frac{{7 - \sqrt {73} }}{{ - 4}}\\\left[ \begin{array}{l}x = \arcsin \frac{{7 - \sqrt {73} }}{{ - 4}} + 2\pi k\\x = \pi - \arcsin \frac{{7 - \sqrt {73} }}{{ - 4}} + 2\pi k\end{array} \right.\\x = \pi - \arcsin \frac{{7 - \sqrt {73} }}{{ - 4}} + 2\pi k,k \in {\bf{Z}}\end{array}\]](/tpl/images/3784/5750/1533c.png)