Ответы на вопрос:
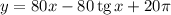
Найдем производную функции:
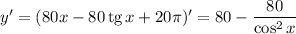
Найдем критические точки функции, приравняв производную к нулю:
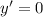
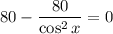
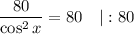
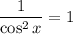
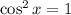
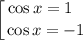

Общее решение: 
Найдем критические точки, которые входят в интервал ![x \in \left[-\dfrac{\pi}{4}; \ \dfrac{\pi}{3} \right]:](/tpl/images/3782/1418/29934.png)
 , то
, то ![x = -\pi \notin \left[-\dfrac{\pi}{4}; \ \dfrac{\pi}{3} \right]](/tpl/images/3782/1418/62dda.png) если
если 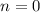 , то
, то ![x = 0 \in \left[-\dfrac{\pi}{4}; \ \dfrac{\pi}{3} \right]](/tpl/images/3782/1418/79209.png) если
если 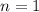 , то
, то ![x = \pi \notin \left[-\dfrac{\pi}{4}; \ \dfrac{\pi}{3} \right]](/tpl/images/3782/1418/c3b13.png)
Найдем значение функции на концах отрезка ![\left[-\dfrac{\pi}{4}; \ \dfrac{\pi}{3} \right]](/tpl/images/3782/1418/7c285.png) и в критической точке
и в критической точке 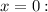
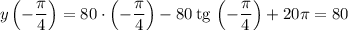
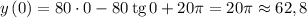
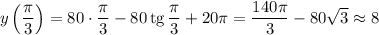
Таким образом, 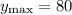
ответ: 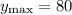
Число делится на 3, если сумма его цифр делится на 3. в число 2*5 можно поставить цифры 2, 2+3=5, 2+6=8. в число 46* можно поставить цифры 2, 5, 8. в число *14 можно поставить цифры 1, 4, 7.
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Математика
-
СТОЛБИКОМ НАДО РЕШИТЬ ЗДЕЛАЙТЕ В ТЕТРАДИ И СУДА ВЫСШЛИТЕ И КТО НАПИШИТ...
 olykylak255101.01.2020 08:07
olykylak255101.01.2020 08:07 -
Решение задачи данута нужно проплыть на тренировке 100 м.Она проплыла 30...
 умник2005605.03.2020 11:13
умник2005605.03.2020 11:13 -
Функциональная математика...
 ForeverDiman12.07.2022 20:53
ForeverDiman12.07.2022 20:53 -
32. Выполните действия, применив правила сло- жения и вычитания смешанных...
 ирина183421.06.2022 05:39
ирина183421.06.2022 05:39 -
Найдите наименьшее значение функции y=x^3-27*x на отрезке [0; 4] найдите...
 полина205419.11.2022 04:03
полина205419.11.2022 04:03 -
За отличную отметку на экзамене ученику подарили конфеты.он так обрадовался...
 plagods21.05.2021 22:32
plagods21.05.2021 22:32 -
Для школьного спорьивног зала купили 16 баскетбольных и футбольных мячей...
 елен927.01.2023 03:49
елен927.01.2023 03:49 -
Исполнители парти юродивого а) козловский б) шаляпин в) пирогов г) нестеренко...
 svetokot200522.03.2020 05:32
svetokot200522.03.2020 05:32 -
От одной станции одновременно отошли в противоположных направлениях отправились...
 Maksim5566611.03.2020 05:26
Maksim5566611.03.2020 05:26 -
Сколько плыть часов на теплоходе из сочи до турции...
 al170a03.09.2021 23:55
al170a03.09.2021 23:55

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.
