Алгебра: Решите уравнение: c^4 - c^3 + c^2 + c = 0

Nekepeshy

14.02.2021 00:59

Алгебра

Есть ответ 👍

Решите уравнение: c^4 - c^3 + c^2 + c = 0

285

422

Посмотреть ответы 3

Ответы на вопрос:

Anna19072003

Алгебра

4,6(74 оценок)

C^3+c^2=0

c^2(c+1)=0

c^2=0 c+1=0

c=0 c=-1

ответ: 0,-1

Санси

Алгебра

4,8(19 оценок)

$0;\;\sqrt[3]{-\dfrac{17}{27}+\sqrt{\dfrac{11}{27}}}+\sqrt[3]{-\dfrac{17}{27}-\sqrt{\dfrac{11}{27}}}+\dfrac{1}{3}$

Объяснение:

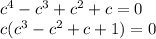
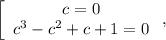
$c^4 - c^3 + c^2 + c = 0\\c(c^3-c^2+c+1)=0$

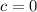
$\left[\begin{array}{c}c=0\\c^3-c^2+c+1=0\end{array}\right,$

c=0

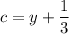Путь $c=y+\dfrac{1}{3}$ .

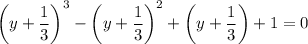
$\left(y+\dfrac{1}{3}\right)^3-\left(y+\dfrac{1}{3}\right)^2+\left(y+\dfrac{1}{3}\right)+1=0$

Упростив выражение получим:

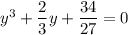
$y^3+\dfrac{2}{3}y+\dfrac{34}{27}=0$

По формуле Кардано, где 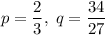$p=\dfrac{2}{3},\;q=\dfrac{34}{27}$ :

$y=\sqrt[3]{-\dfrac{17}{27}+\sqrt{\dfrac{11}{27}}}+\sqrt[3]{-\dfrac{17}{27}-\sqrt{\dfrac{11}{27}}}$

Обратная замена:

$c=\sqrt[3]{-\dfrac{17}{27}+\sqrt{\dfrac{11}{27}}}+\sqrt[3]{-\dfrac{17}{27}-\sqrt{\dfrac{11}{27}}}+\dfrac{1}{3}$

Уравнение решено!

Garri14

Алгебра

4,8(76 оценок)

(sin^2)(8x) = 2(sin^2)(4x)2*[sin(4x)]*[cos(4x)] - 2*sin(4x) = 0[sin(4x)]*[cos(4x) - 1] = 01) sin4x = 0 4x = πn, n∈z x1 = (πn)/4, n∈z 2) cos4x = 1 4x = 2πk, k∈z x2 = (πk)/2, k∈z

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.